Bài 33. Cho \(A, B, C\) là ba điểm của một đường tròn. \(At\) là tiếp tuyến của đường tròn tại \(A\). Đường thẳng song song với \(At\) cắt \(Ab\) tại \(M\) và cắt \(AC\) tại \(N\).
Chứng minh: \(AB. AM = AC . AN\)
Hướng dẫn giải:
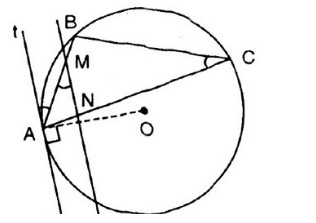
Ta có \(\widehat M = \widehat {BAt}\) (so le trong) (1)
\(\widehat {BAt} = \widehat C\) (2)
(góc tạo bởi tiếp tuyến và dây cung, chắn cung \(AB\), \(\widehat C\) là góc nội tiếp chắn cung \(AB\))
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra:
\(\widehat M = \widehat C\) (3)
Xét hai tam giác \(AMN\) và \(ACB\). chúng có:
\(\widehat A\) chung
\(\widehat M = \widehat C\)
Vậy \(∆AMN\) đồng dạng \(∆ACB\), từ đó \({{AN} \over {AB}} = {{AM} \over {AC}}\),
suy ra \(AB. AM = AC . AN\)
