Bài 36. Cho đường tròn \((O)\) và hai dây \(AB\), \(AC\). Gọi \(M, N\) lần lượt là điểm chính giữa của cung \(AB\) và cung \(AC\). Đường thẳng \(MN\) cắt dây \(AB\) tại \(E\) và cắt dây \(AC\) tại \(H\). Chứng minh rằng tam giác \(AEH\) là tam giác cân.
Hướng dẫn giải:
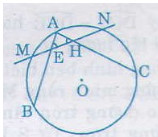
Ta có: \(\widehat {AHM}\)= \(\frac{sđ\overparen{AM}+sđ\overparen{NC}}{2}\) (1)
\(\widehat {AEN}\)= \(\frac{sđ\overparen{MB}+sđ\overparen{AN}}{2}\) (2)
Advertisements (Quảng cáo)
(Vì \widehat {AHM}\)và \(\widehat {AEN}\)là các góc có đỉnh cố định ở bên trong đường tròn).
Theo gỉả thiết thì:
\(\overparen{AM}=\overparen{MB} (3)\)
\(\overparen{NC}=\overparen{AN} (4)\)
Từ (1),(2), (3), (4), suy ra \(\widehat {AHM}\)= \(\widehat {AEN}\) do đó \(∆AEH\) là tam giác cân.
