Qua điểm S nằm bên ngoài đường tròn (O). Bài 40 trang 83 sgk Toán lớp 9 tập 2 - Bài 5. Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
Bài 40. Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn. Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD
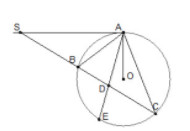
Có: \(\widehat {ADS}=\frac{sđ\overparen{AB}-sđ\overparen{CE}}{2}\) (định lí góc có đỉnh ở ngoài đường tròn).
\(\widehat {SAD}=\frac{1}{2} sđ\overparen{AE}\) (định lí góc giữa tia tiếp tuyến và dây cung).
Advertisements (Quảng cáo)
Có: \(\widehat {BAE} = \widehat {EAC}\) \(\Rightarrow \) \(\overparen{BE}=\overparen{EC}\)
\(\Rightarrow\) \(sđ\overparen{AB}\)+\(sđ\overparen{EC}\)=\(sđ\overparen{AB}+sđ\overparen{BE}\)=
\(sđ\overparen{AE}\)
nên \(\widehat {ADS}=\widehat {SAD}\)\(\Rightarrow\) tam giác \(SDA\) cân tại \(S\) hay \(SA=SD\).