Advertisements (Quảng cáo)
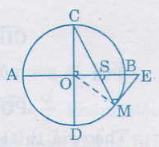
Bài 39. Cho \(AB\) và \(CD\) là hai đường kính vuông góc của đường tròn \((O)\). Trên cung nhỏ \(BD\) lấy một điểm \(M\). Tiếp tuyến tại \(M\) cắt tia \(AB\) ở \(E\), đoạn thẳng \(CM\) cắt \(AB\) ở \(S\).Chứng minh \(ES = EM\).
Hướng dẫn giải:
Ta có \(\widehat{MSE}\) = \(\frac{sđ\overparen{CA}+sđ\overparen{BM}}{2}\) (1)
( vì \(\widehat{MSE}\) là góc có đỉnh S ở trong đường tròn (O))
\(\widehat{CME}\) = \(\frac{sđ\overparen{CM}}{2}\)= \(\frac{sđ\overparen{CB}+sđ\overparen{BM}}{2}\) (2)
Advertisements (Quảng cáo)
(\(\widehat{CME}\) là góc tạo bởi tiếp tuyến và dây cung).
Theo giả thiết \(\overparen{CA}=\overparen{CB}\) (3)
Từ (1), (2), (3) ta có: \(\widehat{MSE}\) = \(\widehat{CME}\) từ đó \(∆ESM\) là tam giác cân và \(ES = EM\)
