Bài 44. Cho tam giác \(ABC\) vuông ở \(A\), có cạnh \(BC\) cố định. Gọi \(I\) là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm \(I\) khi \(A\) thay đổi.
Hướng dẫn giải:
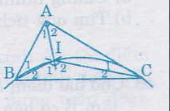
Theo tính chất của góc ngoài tam giác, ta có;
\(\widehat{I_{1}}\) = \(\widehat{A_{1}}\) + \(\widehat{B_{1}}\) (1)
\(\widehat{I_{2}}\) = \(\widehat{A_{2}}\) + \(\widehat{C_{1}}\) (2)
Advertisements (Quảng cáo)
Cộng vế (1) và (2) vế với vế:
\(\widehat{I_{1}}\) +\(\widehat{I_{2}}\) = \(\widehat{A_{1}}\)+\(\widehat{A_{2}}\)+\(\widehat{B_{1}}\)+\(\widehat{C_{1}}\)
Hay \(\widehat{I}\) = \(90^{\circ}\) +\(45^{\circ}\) = \(135^{\circ}\)
Điểm \(I\) nhìn đoạn thẳng \(BC\) cố định dưới góc \(135^{\circ}\) không đổi, vậy quỹ tích của \(I\) là góc cung chứa góc \(135^{\circ}\) dựng trên đoạn thẳng \(BC\).
