Gọi d là đường thẳng đi qua A và song song với BC. + Chứng minh OA là đường trung trực của BC, suy ra \(BC \bot OA\). Gợi ý giải - Bài 2 trang 113 vở thực hành Toán 9 - Bài 16. Vị trí tương đối của đường thẳng và đường tròn. Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A. Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O)...

Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A. Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).

+ Gọi d là đường thẳng đi qua A và song song với BC.
+ Chứng minh OA là đường trung trực của BC, suy ra \(BC \bot OA\).
+ Mà d//BC nên \(d \bot OA\), suy ra d là tiếp tuyến của (O).

Advertisements (Quảng cáo)
(H.5.29)
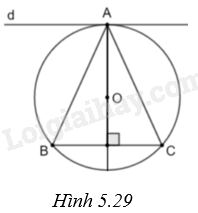
Gọi d là đường thẳng đi qua A và song song với BC.
Ta có: O khác A và \(OB = OC\).
Mặt khác, tam giác ABC cân tại A nên \(AB = AC\).
Từ đó suy ra OA là đường trung trực của BC, tức là \(BC \bot OA\); mà d//BC nên \(d \bot OA\).
Do đó d tiếp xúc với (O) tại A, hay d là tiếp tuyến của (O). (theo dấu hiệu nhận biết tiếp tuyến).
