
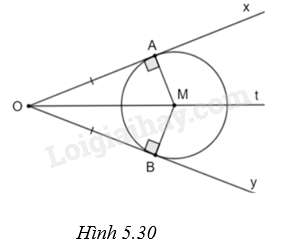
Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho \(OA = OB\). Đường thẳng qua A vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).

+ Theo đề bài, ta có Ox vuông góc với MA tại A nên Ox là tiếp tuyến của (M) tại A.
+ Chứng minh \(\Delta OMA = \Delta OMB\left( {c.c.c} \right)\) nên \(\widehat {MBO} = \widehat {MAO} = {90^o}\).
+ Suy ra OB vuông góc với Oy tại B. Suy ra OB là tiếp tuyến của (M).

(H.5.30)
Advertisements (Quảng cáo)
Theo đề bài, ta có Ox vuông góc với MA tại A nên Ox là tiếp tuyến của (M) tại A.
Do Ot là tia phân giác của góc xOy và \(M \in Ot\) nên \(MA = MB\).
Hai tam giác OMA và OMB có: cạnh OM chung; \(MA = MB\); \(OA = OB\).
Do đó \(\Delta OMA = \Delta OMB\left( {c.c.c} \right)\).
Suy ra \(\widehat {MBO} = \widehat {MAO} = {90^o}\), tức là OB vuông góc với MB tại B.
Do vậy OB là tiếp tuyến của (M) (theo dấu hiệu nhận biết tiếp tuyến).
