
Cho tam giác ABC cân tại A có ba đỉnh nằm trên đường tròn (O). Đường cao AH cắt (O) tại D. Biết \(BC = 24cm,AC = 20cm\). Tính chiều cao AH và bán kính đường tròn (O).

+ Chứng minh H là trung điểm của BC nên tính được HC.
+ Tam giác ACH vuông tại H nên theo định lý Pythagore, ta tính được AH.
+ Chứng minh tam giác ACD vuông tại C.
+ Trong tam giác ACD vuông tại C ta có: \(A{C^2} = AH.AD\) nên tính được AD
+ Bán kính của đường tròn (O) là \(R = \frac{{AD}}{2}\).
Advertisements (Quảng cáo)

(H.5.5)
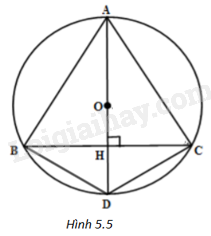
Vì tam giác ABC cân tại A nên đường cao AH cũng là đường trung trực của đoạn BC, suy ra H là trung điểm của BC.
Tam giác ACH vuông tại H nên theo định lý Pythagore, ta được \(A{H^2} = A{C^2} - H{C^2}\), suy ra \(AH = 16cm\).
Tam giác ACD có AD là đường kính của đường tròn (O) nên tam giác ACD vuông tại C.
Trong tam giác ACD vuông tại C ta có: \(A{C^2} = AH.AD\), suy ra \(AD = \frac{{A{C^2}}}{{AH}} = 25cm\).
Vậy bán kính của đường tròn (O) là \(R = \frac{{AD}}{2} = \frac{{25}}{2}cm\).
