Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r < OO' < R + r\). Lời giải bài tập, câu hỏi - Bài 5 trang 118 vở thực hành Toán 9 - Bài 17. Vị trí tương đối của hai đường tròn. Cho hai đường tròn (O; R) và (O’; r) với (R = 12cm, r = 5cm, OO' = 13cm). a) Chứng minh hai đường tròn (O) và (O’) cắt nhau tại hai điểm A...
Cho hai đường tròn (O; R) và (O’; r) với \(R = 12cm,r = 5cm,OO’ = 13cm\).
a) Chứng minh hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B và OO’ là đường trung trực của AB.
b) Chứng minh AO là tiếp tuyến của (O’, r).
a) Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r
b) Sử dụng định lý Pythagore đảo để chứng minh tam giác AOO’ vuông tại A. Do đó, \(OA \bot O’A\) tại A. Do đó, AO là tiếp tuyến của (O’; r).
Advertisements (Quảng cáo)
(H.5.38)
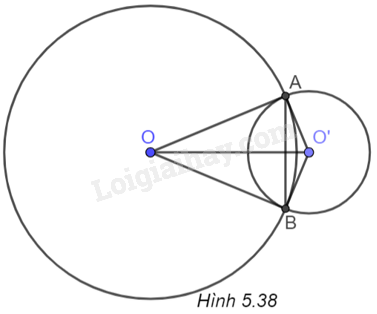
a) Vì \(12 - 5
Ta có: \(OA = OB = R\) và \(O’A = O’B = r\) nên OO’ là đường trung trực của AB.
b) Ta có: \(OO{‘^2} = {13^2} = 169 = {5^2} + {12^2} = O{A^2} + O'{A^2}\) nên tam giác AOO’ vuông tại A (theo định lý Pythagore đảo), suy ra \(OA \bot O’A\) tại A. Do đó, AO là tiếp tuyến của (O’; r).