Câu hỏi trắc nghiệm trang 116 vở thực hành Toán 9: Cho hai đường tròn (O; R) và (O’; r) với \(R > r\) cắt nhau tại hai điểm phân biệt và \(OO’ = d\)...

Chọn phương án đúng trong mỗi câu sau:

Câu 1

Cho hai đường tròn (O; R) và (O’; r) với \(R > r\) cắt nhau tại hai điểm phân biệt và \(OO’ = d\). Khẳng định nào sau đây là đúng?

A. \(d = R - r\).

B. \(d > R + r\).

C. \(R - r

D. \(d

Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r

Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r

Chọn C

Câu 2

Cho hai đường tròn (O; 5cm) và (O’; 3cm) với \(OO’ = 12cm\). Khẳng định nào sau đây đúng về vị trí tương đối của hai đường tròn?

A. Hai đường tròn cắt nhau.

B. Hai đường tròn tiếp xúc ngoài.

C. Hai đường tròn ở ngoài nhau.

D. Hai đường tròn tiếp xúc trong.

Hai đường tròn (O; R) và (O’; r) ở ngoài nhau khi \(OO’ > R + r\).

Vì \(5 + 3 = 8

Chọn C

Câu 3

Cho hai đường tròn (O; 4cm) và (O’; R cm) tiếp xúc ngoài nhau biết \(OO’ = 10cm\). Khi đó:

A. \(R = 4cm\).

B. \(R = 14cm\).

C. \(R = 10cm\).

D. \(R = 6cm\).

Hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài khi \(OO’ = R + r\).

Vì hai đường tròn (O; 4cm) và (O’; R cm) tiếp xúc ngoài nhau nên \(OO’ = 4 + R\), suy ra \(10 = 4 + R\) nên \(R = 6cm\)

Chọn D

Câu 4

Cho hai đường tròn (O) và (O’) cắt nhau tại A và B trong đó OA là tiếp tuyến của (O’). Biết rằng \(OA = 20cm\) và \(O’A = 15cm\). Độ dài dây AB là:

A. 24cm.

B. 12cm.

C. 25cm.

D. 22cm.

+ Chứng minh tam giác O’AO vuông tại A. Theo định lý Pythagore tính được OO.

+ Chứng minh OO’ là đường trung trực của AB.

+ Gọi I là giao điểm của OO’ và AB. Khi đó, \(AI = \frac{1}{2}AB\) và \(AI \bot OO’\).

+ Ta có: \(AI.OO’ = O’A.AO\left( { = 2.{S_{\Delta O’AO}}} \right)\), từ đó tính được AI, do đó tính được AB.

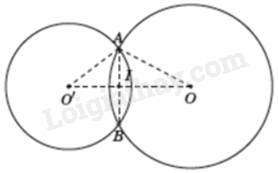
Vì OA là tiếp tuyến của (O’) nên \(O’A \bot OA\). Do đó, tam giác OAO’ vuông tại A. Theo định lý Pythagore ta có: \(OO{‘^2} = O{A^2} + O'{A^2} = {20^2} + {15^2} = 625\) nên \(OO’ = 25cm\).

Ta có \(OA = OB\) (bán kính (O)) nên O thuộc đường trung trực của AB, \(O’A = O’B\) (bán kính (O’)) nên O’ thuộc đường trung trực của AB. Do đó, OO’ là đường trung trực của AB.

Gọi I là giao điểm của OO’ và AB. Khi đó, \(AI = \frac{1}{2}AB\) và \(AI \bot OO’\).

Ta có: \(AI.OO’ = O’A.AO\left( { = 2.{S_{\Delta O’AO}}} \right)\) nên \(AI = \frac{{O’A.OA}}{{OO’}} = \frac{{15.20}}{{25}} = 12\left( {cm} \right)\). Do đó, \(AB = 2AI = 24cm\)

Chọn A