
Cho đường tròn tâm O, bán kính R. Từ điểm A nằm ngoài đường tròn vẽ hai tiếp tuyến AB, AC với dường tròn tâm O; B, C là các tiếp điểm.
a) Chứng minh AO là đường trung trực của BC.
b) Kẻ đường kính CD. Chứng minh BD song song với AO.
c) Kẻ OM vuông góc với OB (M thuộc AC). Chứng minh \(MO = MA\).

a) + Chứng minh \(AB = AC\) nên A thuộc đường trung trực của đoạn thẳng BC.
+ Chứng minh \(OB = OC\) nên O thuộc đường trung trực của đoạn thẳng BC.
+ Do đó, OA là trung trực của BC
b) Chứng minh tam giác BCD vuông tại B, suy ra \(BD \bot BC\). Mà \(AO \bot BC\) nên BD // AO.
c) + Chứng minh \(\widehat {MOA} + \widehat {AOB} = {90^o}\), \(\widehat {MAO} = \widehat {BAO}\), \(\widehat {MAO} + \widehat {BOA} = {90^o}\) nên \(\widehat {MOA} = \widehat {MAO}\).
+ Chứng minh \(\Delta AMO\) cân tại M nên \(MO = MA\).
Advertisements (Quảng cáo)

(H.5.32)
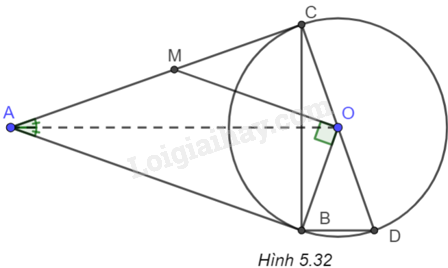
a) Xét hai tiếp tuyến AB, AC của (O) cắt nhau tại A, ta có \(AB = AC\) nên A thuộc đường trung trực của đoạn thẳng BC. Mặt khác, \(OB = OC\) (cùng bằng bán kính). Do đó O thuộc đường trung trực của đoạn thẳng BC.
Vậy OA là đường trung trực của BC.
b) Xét tam giác BCD có BO là đường trung tuyến, \(BO = \frac{1}{2}CD\), suy ra tam giác CBD vuông tại B, hay \(BD \bot BC\). Mặt khác \(AO \bot BC\) (do AO là đường trung trực của BC)
Từ đó suy ra BD song song với AO.
c) Theo giả thiết, ta có \(OM \bot OB\), suy ra \(\widehat {MOA} + \widehat {AOB} = {90^o}\). (1)
Ta có \(\widehat {MAO} = \widehat {BAO}\) (do A là giao điểm của hai tiếp tuyến của (O))
Vì AB là tiếp tuyến của (O) nên \(AB \bot OB\). Do đó, \(\widehat {OAB} + \widehat {AOB} = {90^o}\), suy ra \(\widehat {MAO} + \widehat {BOA} = {90^o}\) (2)
Từ (1) và (2) suy ra: \(\widehat {MOA} = \widehat {MAO}\), do đó \(\Delta AMO\) cân tại M nên \(MO = MA\).
