
Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng \(N{80^ \circ }E\) với vận tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng\(E{20^ \circ }S\) giữ nguyên vận tốc và chạy tiếp 36 phút nữa đến đảo Cát Bà. Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu ki lô mét.

- Đổi 30 phút = \(\frac{1}{2}\) giờ và 36 phút = \(\frac{3}{5}\) giờ
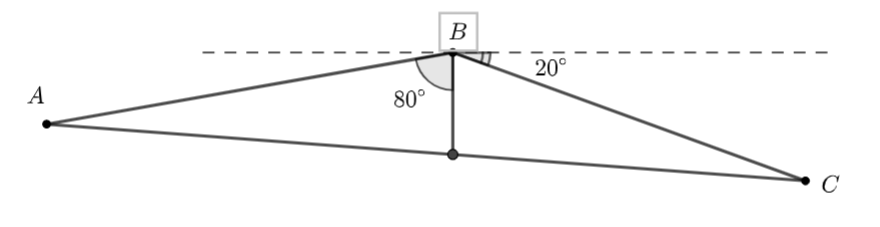
- Tính \(\widehat {ABC}\)
- Tính quãng đường \(AB,\,\,BC\)
- Áp dụng định lý côsin để tính quãng đường \(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos ABC\)
Advertisements (Quảng cáo)

Xét \(\Delta ABC\) có \(\widehat B = {80^ \circ } + \left( {{{90}^ \circ } - {{20}^ \circ }} \right) = {150^ \circ }.\)
Độ dài quãng đường \(AB\) là: \(AB = 20.\frac{1}{2} = 10\,\,km.\)
Độ dài quãng đường \(BC\) là: \(BC = 20.\frac{3}{5} = 12\,\,km.\)
Khoảng cách từ điểm xuất phát A đến điểm đích C là:
Áp dụng định lý côsin, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos ABC\\A{C^2} = {10^2} + {12^2} - 2.10.12.\cos {150^ \circ }\\A{C^2} = 100 + 144 - 240.\left( {\frac{{ - \sqrt 3 }}{2}} \right) \approx 452.\\ \Rightarrow \,\,AC \approx \sqrt {452} \approx 21\,\,km.\end{array}\)
