Giải bài 4.43 trang 67 sách bài tập toán 10 - Kết nối tri thức với cuộc sống - Bài tập cuối chương IV

Cho tam giác \(ABC\) đều, trọng tâm \(G,\) có độ dài các cạnh bằng 3. Độ dài vectơ \(\overrightarrow {AG} \) bằng
A. \(\sqrt 3 \)
B. \(\frac{{3\sqrt 3 }}{2}\)
C. \(\frac{{\sqrt 3 }}{2}\)
D. \(2\sqrt 3 \)
Advertisements (Quảng cáo)

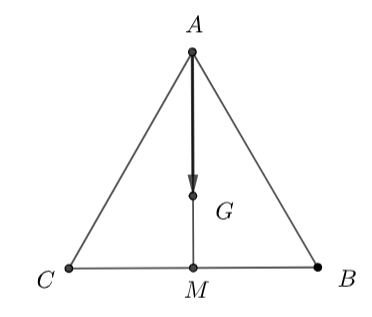
Gọi \(M\) là trung điểm của cạnh \(BC\)
\( \Rightarrow \) \(AM = \frac{{3\sqrt 3 }}{2}\)
Xét \(\Delta ABC\) đều có \(G\) là trọng tâm của tam giác
\( \Rightarrow \) \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} \)
\( \Rightarrow \left| {\overrightarrow {AG} } \right| = \frac{2}{3}\left| {\overrightarrow {AM} } \right| = \frac{2}{3}.\frac{{3\sqrt 3 }}{2} = \sqrt 3 \)
Chọn A.
