Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng:
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = {2 \over 3}\overrightarrow {MO} \)
Gợi ý làm bài
(Xem hình 1.73)
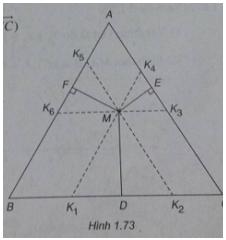
Qua M kẻ các đường thẳng sau: \({K_1}{K_4}\)//AB, \({K_2}{K_5}\)//AC, \({K_3}{K_6}\)//BC
Advertisements (Quảng cáo)
\({K_1},{K_2} \in BC;{K_3},{K_4} \in AC;{K_5},{K_6} \in AB\). Ta có:
\(\eqalign{
& \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} \cr
& = {1 \over 2}(\overrightarrow {M{K_1}} + \overrightarrow {M{K_2}} + \overrightarrow {M{K_3}} + \overrightarrow {M{K_4}} + \overrightarrow {M{K_5}} + \overrightarrow {M{K_6}} ) \cr} \)
\( = {1 \over 2}(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} )\)
(Vì \(M{K_5}A{K_4},M{K_3}C{K_2},M{K_1}B{K_6}\) là các hình bình hành). Vậy
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = {1 \over 2}.3\overrightarrow {MO} = {3 \over 2}\overrightarrow {MO} \)
