Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có AB: 3x + 5y - 33 = 0; đường cao AH: 7x + y - 13 = 0; trung tuyến BM: x + 6y - 24 = 0 (M là trung điểm của AC). Tìm phương trình các cạnh còn lại của tam giác.
Gợi ý làm bài
(Xem hình 3.38)
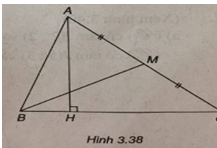
Tọa độ điểm A là nghiệm của hệ phương trình:
\(\left\{ \matrix{
3x + 5y - 33 = 0\,\,\,\,\,\,\,(AB) \hfill \cr
7x + y - 13 = 0\,\,\,\,\,\,\,\,\,(AH). \hfill \cr} \right.\)
Vậy A(1 ; 6)
Tọa độ điểm B là nghiệm của hệ phương trình:
\(\left\{ \matrix{
3x + 5y - 33 = 0\,\,\,\,\,\,\,(AB) \hfill \cr
x + 6y - 24 = 0\,\,\,\,\,\,\,\,\,(BM) \hfill \cr} \right.\)
Vậy B(6 ; 3).
Advertisements (Quảng cáo)
Đặt C(x;y) ta suy ra trung điểm M của AC có tọa độ \(M\left( {{{x + 1} \over 2};{{y + 6} \over 2}} \right).\)
Ta có: \(\overrightarrow {BC} = \left( {x - 6;y - 3} \right)\)
\({\overrightarrow u _{AH}} = (1; - 7)\)
Ta có: \(\left\{ \matrix{
M \in BM \hfill \cr
\overrightarrow {BC} .{\overrightarrow u _{AH}} = 0 \hfill \cr} \right.\)
Suy ra tọa độ điểm C là nghiệm của hệ phương trình:
\(\left\{ \matrix{
\left( {{{x + 1} \over 2}} \right) + 6\left( {{{y + 6} \over 2}} \right) \hfill \cr
x - 6 - 7(y - 3) = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{
x + 6y - 11 = 0 \hfill \cr
x - 7y + 15 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 1 \hfill \cr
y = 2. \hfill \cr} \right.\)
Vậy C(-1 ; 2).
Phương trình cạnh BC: x - 7y + 15 = 0
Phương trình cạnh AC: 2x - y + 4 = 0.
