Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có \({x_A} = 2\), điểm C và trung điểm K của AD cùng thuộc trục Oy, tâm I thuộc trục Ox, AD = 2AB. Tìm tọa độ các đỉnh của hình chữ nhật ABCD, biết rằng K có tung độ âm.
Gợi ý làm bài
(Xem hình 3.45)
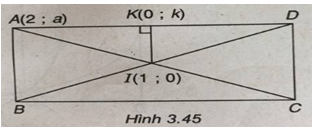
Đặt A(2 ; a); K(0 ; k); C(0 ; c); I(1 ; 0) là tọa độ các điểm đã cho ta có:
\({{a + c} \over 2} = 0 \Rightarrow c = - a.\)
\(AD = 2AB \Rightarrow AK = 2KI.\) Ta có: \(\overrightarrow {AK} = ( - 2;k - 1),\,\overrightarrow {IK} = ( - 1;k)\)
\(\left\{ \matrix{
\overrightarrow {AK} .\overrightarrow {IK} = o \hfill \cr
\left| {\overrightarrow {AK} } \right| = 2\left| {\overrightarrow {IK} } \right| \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2 + k(k - a) = 0 \hfill \cr
{\overrightarrow {AK} ^2} = 4{\overrightarrow {IK} ^2} \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
k - a = - {k \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \cr
4 + {(k - a)^2} = 4(1 + {k^2})\,\,\,\,(2) \hfill \cr} \right.\)
Thay (1) vào (2) ta được:
Advertisements (Quảng cáo)
\(\eqalign{
& 4 + {4 \over {{k^2}}} = 4\left( {1 + {k^2}} \right) \cr
& \Leftrightarrow 4{k^2} + 4 = 4{k^2} + 4{k^4} \cr
& \Leftrightarrow {k^2} = 1 \Leftrightarrow k = - 1\,\,(k < 0). \cr} \)
Suy ra a = -3.
Vậy A(2 ; -3), C(0 ; 3) và K(0 ; -1).
Ta có:
\(\eqalign{
& \overrightarrow {AD} = 2\overrightarrow {AK} \Rightarrow \left\{ \matrix{
{x_D} - 2 = 2.(0 - 2) \hfill \cr
{y_D} + 3 = 2.( - 1 + 3) \hfill \cr} \right. \cr
& \Rightarrow \left\{ \matrix{
{x_D} = 2 \hfill \cr
{y_D} = 1. \hfill \cr} \right. \cr} \)
Vậy D(-2 ; 1)
Ta có:
\(\eqalign{
& \overrightarrow {DB} = 2\overrightarrow {DI} \Rightarrow \left\{ \matrix{
{x_B} + 2 = 2.(1 + 2) \hfill \cr
{y_B} - 1 = 2.(0 - 1) \hfill \cr} \right. \cr
& \Rightarrow \left\{ \matrix{
{x_B} = 4 \hfill \cr
{y_B} = - 1. \hfill \cr} \right. \cr} \)
Vậy B(4 ; -1).
