Trong mặt phẳng tọa độ Oxy, lập phương trình chính tắc của elip (E) biết (E) có tiêu điểm \({F_1}\left( { - 2;0} \right)\) và diện tích hình chữ nhật cơ sở bằng \(12\sqrt 5 \)
Viết phương trình đường tròn (C) có tâm là gốc tọa độ và (C) cắt (E) tại bốn điểm tạo thành hình vuông.
Gợi ý làm bài
(Xem hình 3.44)
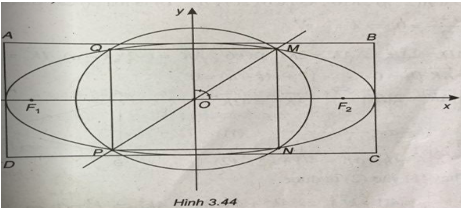
Phương trình elip có dạng: \((E):{{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1.\)
Ta có tiêu điểm \({F_1}\left( { - 2;0} \right)\). Suy ra c = 2.
Diện tích hình chữ nhật cơ sở ABCD là 4ab. Suy ra \(4ab = 12\sqrt 5 \)
Ta có : \({a^2} = {b^2} + {c^2} = {b^2} + 4.\)
Giải hệ phương trình :
Advertisements (Quảng cáo)
\(\left\{ \matrix{
ab = 3\sqrt 5 \hfill \cr
{a^2} = {b^2} + 4 \hfill \cr} \right.\)
Ta được:
\(\left\{ \matrix{
a = 3 \hfill \cr
b = \sqrt 5 . \hfill \cr} \right.\)
Vậy phương trình elip là : \({{{x^2}} \over 9} + {{{y^2}} \over 5} = 1.\)
Đường tròn (C) tâm O, bán kính R cắt elip tại bốn điểm M, N, P, Q.
Ta có MNPQ là hình vuông suy ra phương trình đường thẳng OM là : y = x.
Thay y = x vào phương trình elip ta được:
\({R^2} = O{M^2} = x_M^2 + y_M^2 = {{45} \over 7}.\)
Vậy phương trình đường tròn (C) là : \({x^2} + {y^2} = {{45} \over 7}\)
