Trong mặt phẳng tọa độ Oxy, cho hai đường tròn:
(C1) : \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\)
và (C2) : \({\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 16\)
a) Chứng minh rằng hai đường tròn (C1) , (C2) cắt nhau ;
b) Tìm tọa độ giao điểm của hai tiếp tuyến chung của (C1) và (C2).
Gợi ý làm bài
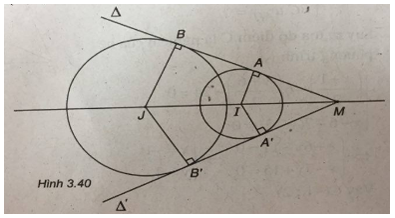
(Xem hình 3.40)
a) (C1) có tâm I(2 ; 2) và bán kính \({R_1} = 2\)
(C2) có tâm J(5 ; 3) và bán kính \({R_2} = 4\)
Advertisements (Quảng cáo)
Ta có:
\(IJ = \sqrt {{{\left( {5 - 2} \right)}^2} + {{\left( {3 - 2} \right)}^2}} = \sqrt {10} .\)
Do: \({R_2} - {R_1} < IJ < {R_2} + {R_1}\)
Nên (C1) và (C2) cắt nhau tại hai điểm phân biệt.
b) Gọi \(\Delta \) và \(\Delta’ \) là hai tiếp tuyến chung của (C1) và (C2) . \(\Delta \) tiếp xúc với (C1) và (C2) lần lượt tại A, B. \(\Delta’ \) tiếp xúc với (C1) và (C2) lần lượt tại A’, B’.
Ta có:
\(\left\{ \matrix{
d(I,\Delta ) = d(I,{\Delta’}) = {R_1} = 2 \hfill \cr
d(J,\Delta ) = d(J,{\Delta’}) = {R_2} = 4 \hfill \cr} \right. \Rightarrow IJ,\Delta \) và \(\Delta’ \) đồng quy tại M.
\(\eqalign{
& {{JM} \over {IM}} = {{JB} \over {IA}} = {{{R_2}} \over {{R_1}}} = 2 \cr
& \Rightarrow \overrightarrow {JM} = 2\overrightarrow {JI} \cr
& \Rightarrow \left\{ \matrix{
{x_M} - 5 = 2.\left( {2 - 5} \right) \hfill \cr
{y_M} - 3 = 2.(2 - 3 \hfill \cr} \right. \cr
& \Rightarrow \left\{ \matrix{
{x_M} = - 1 \hfill \cr
{y_M} = 1. \hfill \cr} \right. \cr} \)
Vậy ta được M(-1 ; 1).
