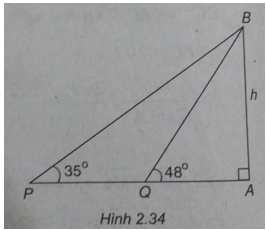
Hai chiếc tàu thủy P và Q cách nhau 300m. Từ P và Q thẳng hàng với chân A của tháp hải đẳng AB trên bờ biển người ta nhìn chiều cao AB của tháp dưới các góc \(\widehat {BPA} = {35^o}\) và \(\widehat {BQA} = {48^ô}\)
a)Tính BQ;
b)Tính chiều cao của tháp.
Gợi ý làm bài
a) (Xem hình 2.34)
Advertisements (Quảng cáo)
Ta có: \(\widehat {PBQ} = {48^ \circ } - {35^ \circ } = {13^ \circ }\)
Trong tam giác BPQ ta có:
\({{BQ} \over {\sin P}} = {{PQ} \over {\sin B}} \Leftrightarrow {{BQ} \over {\sin {{35}^ \circ }}} = {{300} \over {\sin {{13}^ \circ }}}\)
Do đó: \(BQ = {{300.\sin {{35}^ \circ }} \over {\sin {{13}^ \circ }}} \approx 764,935(m)\)
b) Chiều cao của tháp là
\(\eqalign{
& AB = BQ\sin {48^ \circ } \cr
& \approx 764,935.\sin {48^ \circ } \approx 568,457(m) \cr} \)
