Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({(x - 1)^2} + {(y - 2)^2} = 4\) và đường thẳng d: x - y - 1 = 0. Viết phương trình đường tròn (C ’) đối xứng vơi đường tròng (C) qua đường thẳng d. Tìm tọa độ các giao điểm của (C ’) và (C).
Gợi ý làm bài
(Xem hình 3.23)
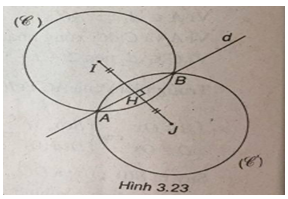
Đường thẳng d có vectơ pháp tuyến là \(\overrightarrow n = \left( {1; - 1} \right).\) Do đó đường thẳng \(\Delta \) đi qua tâm \(I\left( {1;2} \right)\) và vuông góc với d có phương trình :
\({{x - 1} \over 1} = {{y - 2} \over { - 1}} \Leftrightarrow x + y - 3 = 0.\)
Tọa độ giao điểm H của d và là nghiệm của hệ phương trình :
\(\left\{ \matrix{
x - y - 1 = 0 \hfill \cr
x + y - 3 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 2 \hfill \cr
y = 1 \hfill \cr} \right. \Rightarrow H\left( {2;1} \right)\)
Gọi J là điểm đối xứng của I qua d. Khi đó :
Advertisements (Quảng cáo)
\(\left\{ \matrix{
{x_J} = 2{x_H} - {x_I} = 3 \hfill \cr
{y_J} = 2{y_H} - {y_I} = 0 \hfill \cr} \right. \Rightarrow J(3;0).\)
Vì (C ’) đối xứng với (C ) qua d nên (C ’) có tâm là \(J\left( {3;0} \right)\) và bán kính R = 2.
Do đó (C ’) có phương trình là :
\({\left( {x - 3} \right)^2} + {y^2} = 4\)
Tọa độ các giao điểm của (C ) và (C ’) là nghiệm của hệ phương trình :
\(\left\{ \matrix{
{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4 \hfill \cr
{\left( {x - 3} \right)^2} + {y^2} = 4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x - y - 1 = 0 \hfill \cr
{\left( {x - 3} \right)^2} + {y^2} = 4 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{
y = x - 1 \hfill \cr
2{x^2} - 8x + 6 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 1,y = 0 \hfill \cr
x = 3,y = 2. \hfill \cr} \right.\)
Vậy tọa độ giao điểm của (C ) và (C ’) là A(1 ; 0) và B(3 ; 2).
