Trong mặt phẳng tọa độ Oxy,xét tam giác ABC vuông tại A, phương trình đường thẳng BC là : \(\sqrt 3 x - y - \sqrt 3 = 0\), các đỉnh A và B thuộc trục hoành và bán kính đường tròn nội tiếp tam giác bằng 2. Tìm tọa độ trọng tâm G của tam giác ABC.
Gợi ý làm bài
( Xem hình 3.25)
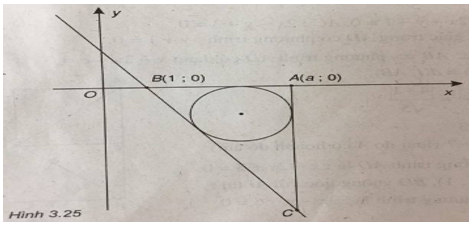
Ta có: \(BC \cap Ox = B(1;0)\)
Đặt \({x_A} = a\) ta có A(a;0) và \({x_C} = a \Rightarrow {y_C} = \sqrt 3 a - \sqrt 3 .\)
Vậy \(C\left( {a;\sqrt 3 a - \sqrt 3 } \right).\)
Từ công thức
\(\left\{ \matrix{
{x_G} = {1 \over 3}\left( {{x_A} + {x_B} + {x_C}} \right) \hfill \cr
{y_G} = {1 \over 3}\left( {{y_A} + {y_B} + {y_C}} \right) \hfill \cr} \right.\)
Ta có:
Advertisements (Quảng cáo)
\(G\left( {{{2a + 1} \over 3};{{\sqrt 3 \left( {a - 1} \right)} \over 3}} \right).\)
Mà \(AB = \left| {a - 1} \right|,AC = \sqrt 3 \left| {a - 1} \right|,BC = 2\left| {a - 1} \right|\). Do đó :
\({S_{\Delta ABC}} = {1 \over 2}AB.AC = {{\sqrt 3 } \over 2}{\left( {a - 1} \right)^2}.\)
Ta có:
\(\eqalign{
& r = {{2S} \over {AB + AC + BC}} \cr
& = {{\sqrt 3 {{\left( {a - 1} \right)}^2}} \over {3\left| {a - 1} \right| + \sqrt 3 \left| {a - 1} \right|}} = {{\left| {a - 1} \right|} \over {\sqrt 3 + 1}} = 2. \cr} \)
Vậy \(\left| {a - 1} \right| = 2\sqrt 3 + 2.\)
Trường hợp 1.
\({a_1} = 2\sqrt 3 + 3 \Rightarrow {G_1}\left( {{{7 + 4\sqrt 3 } \over 3};{{6 + 2\sqrt 3 } \over 3}} \right).\)
Trường hợp 2.
\({a_2} = - 2\sqrt 3 - 1 \Rightarrow {G_2}\left( {{{4\sqrt 3 - 1} \over 3};{{ - 6 - 2\sqrt 3 } \over 3}} \right).\)
