Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng: \({d_1}:x - y = 0\) và \({d_2}:2x + y - 1 = 0\) Tìm tọa độ các đỉnh hình vuông ABCD biết rằng đỉnh A thuộc \({d_1}\) , đỉnh C thuộc \({d_2}\) và các đỉnh B, D thuộc trục hoành.
Gợi ý làm bài
(Xem hình 3.21)
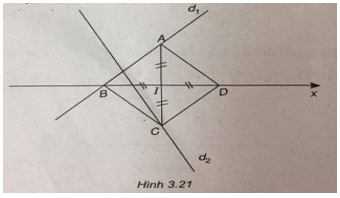
Vì \(A \in {d_1} \Rightarrow A\left( {t;t} \right).\)
Vì A và C đối xứng nhau qua BD và \(B,D \in Ox\) nên \(C\left( {t; - t} \right)\)
Vì \(C \in {d_2}\) nên \(2t - t - 1 = 0 \Leftrightarrow t = 1\). Vậy A(1 ; 1), C(1 ; -1).
Advertisements (Quảng cáo)
Trung điểm AC là I(1 ; 0). Vì I là tâm hình vuông nên
\(\left\{ \matrix{
IB = IA = 1 \hfill \cr
ID = IA = 1 \hfill \cr} \right.\)
\(\eqalign{
& \left\{ \matrix{
B \in Ox \hfill \cr
D \in Ox \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
B(b;0) \hfill \cr
D(d;0) \hfill \cr} \right. \cr
& \Rightarrow \left\{ \matrix{
\left| {b - 1} \right| = 1 \hfill \cr
\left| {d - 1} \right| = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
b = 0,b = 2 \hfill \cr
d = 0,d = 2. \hfill \cr} \right. \cr} \)
Suy ra B(0 ; 0) và D(2 ; 0) hoặc B(2 ; 0), D(0 ; 0).
Vậy bốn đỉnh của hình vuông là A(1 ; 1), B(0 ; 0), C(1 ; -1), D(2 ; 0)
hoặc A(1 ; 1), B(2 ; 0), C(1 ; -1), D(0 ; 0).
