Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) . Bài 3.61 trang 164 Sách bài tập (SBT) Toán Hình Học 10 - Ôn tập chương III: Đề toán tổng hợp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\) và đường thẳng d: 3x - 4y + m = 0. Tìm m để trên d có duy nhất một điểm P mà từ đó có thể kẻ được hai tiếp tuyến PA, PB tới (C) (A, B là các tiếp điểm) sao cho tam giác PAB đều.
Gợi ý làm bài
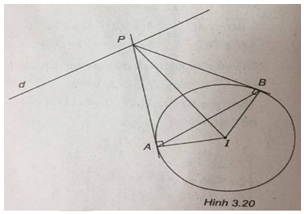
(Xem hình 3.20)
Advertisements (Quảng cáo)
(C) có tâm I(1 ; -2) và bán kính R = 3. Ta có tam giác PAB đều thì \(IP = 2IA = 2R = 6 \Leftrightarrow P\) thuộc đường tròn (C ’) có tâm I, bán kính R’=6.
Trên d có duy nhất một điểm P thỏa mãn yêu cầu bài toán khi và chỉ khi d tiếp xúc với (C ’) tại P \( \Leftrightarrow d(I,d) = 6\)
\( \Leftrightarrow m = 19,\,\,m = - 41.\)