a) Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau
\(y = f(x) = \left| {x + 3} \right| - 1\);
\(y = g(x) = \left| {2x - m} \right|\); trong đó m là tham số
Xác định hoành độ các giao điểm của mỗi đồ thị với trục hoành.
b) Tìm các giá trị của tham số m để bất phương trình sau nghiệm đúng với mọi giá trị của x
\(\left| {2x - m} \right| > \left| {x + 3} \right| - 1\)
Gợi ý làm bài
Advertisements (Quảng cáo)
a) Đồ thị hàm số y = f(x) là đường gấp khúcu’Eu, cắt Ox tại A(-4; 0) và B(-2;0).
Đồ thị hàm số y = g(x) là đường gấp khúc v’Cv, cắt Ox tại \(C({m \over 2};0)\)
Khi m thay đổi, điểm C chạy trên Ox; tia Cv luông song song với đường thẳng y = 2x; tia Cv’ luôn song song với đường thẳng y = -2x.
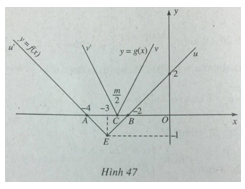
b) Bất phương trình đã cho đúng với mọi x khi và chỉ khi đồ thị của hàm số y = g(x) nằm hoàn toàn phía trên đồ thị của hàm số y = f(x) hay C nằm giữa A và B nghĩa là \( - 4 < {m \over 2} < - 2 \Leftrightarrow - 8 < m < - 4\)
Đáp số: \( - 8 < m < - 4\)
