
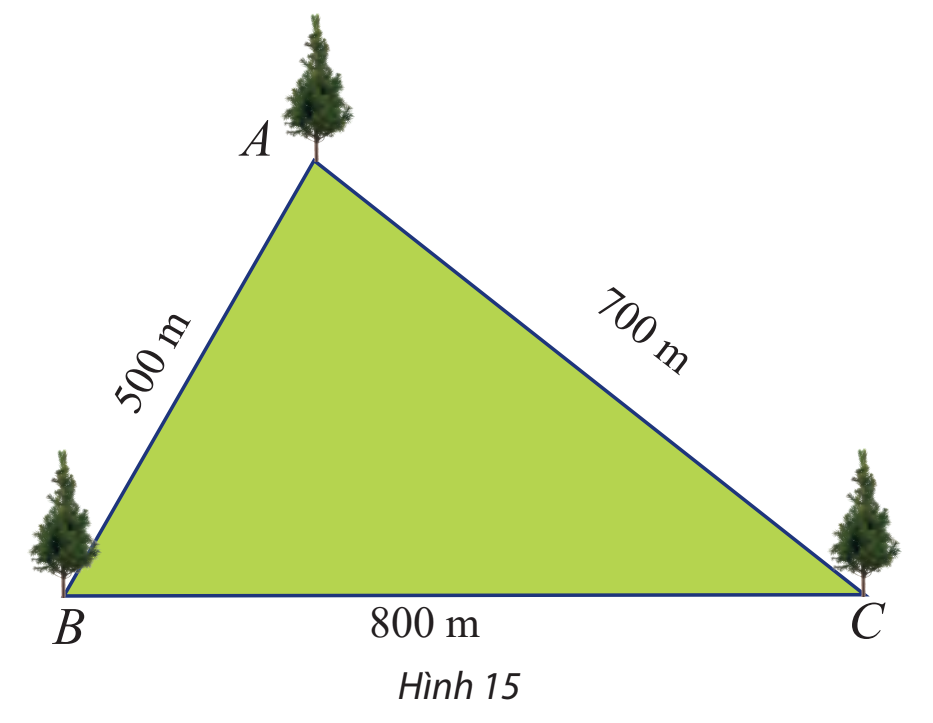
Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.

Áp dụng định lí cosin để tính góc:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.\)
Advertisements (Quảng cáo)

Đặt \(a = BC,b = AC,c = AB\)
Ta có: \(a = 800,b = 700,c = 500.\)
Áp dụng định lí cosin, ta có:
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}.\)
Suy ra:
\(\begin{array}{l}\cos A = \frac{{{{700}^2} + {{500}^2} - {{800}^2}}}{{2.700.500}} = \frac{1}{7} \Rightarrow \widehat A = {81^o}47’12,44”;\\\cos B = \frac{{{{500}^2} + {{800}^2} - {{700}^2}}}{{2.500.800}} = \frac{1}{2} \Rightarrow \widehat B = {60^o};\\\cos C = \frac{{{{800}^2} + {{700}^2} - {{500}^2}}}{{2.800.700}} = \frac{{11}}{{14}} \Rightarrow \widehat C = {38^o}12’47,56”.\end{array}\)
Vậy \(\widehat A = {81^o}47’12,44”;\widehat B = {60^o};\widehat C = {38^o}12’47,56”.\)
