Cho \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\) và hypebol \((H):{{{x^2}} \over 5} - {{{y^2}} \over 4} = 1.\)
a) Tìm tọa độ các tiêu điểm của (E) và (H).
b) Vẽ phác elip (E) và hypebol (H) trong cùng một hệ trục tọa độ.
c) Tìm tọa độ các giao điểm của (E) và (H).

a) Với \((E):{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1\) ta có \(a = \sqrt 5 \,\,\,b = 2\,\,\, \Rightarrow \,c = \sqrt {{a^2} - {b^2}} = 1\)
Tọa độ các tiêu điểm của (E) là \({F_1}( - 1\,;\,0)\,\,\,{F_2}(1\,;\,0)\)
Advertisements (Quảng cáo)
Với (H) : \({{{x^2}} \over 5} - {{{y^2}} \over 4} = 1\) , ta có \(a = \sqrt 5 \,\,b = 2\,\,\,c = \sqrt {{a^2} + {b^2}} = 3\)
Tọa độ các tiêu điểm của (H) là \({F_1}( - 3\,;\,0)\,\,\,{F_2}(3\,;\,0)\)
b) Vẽ (E) và (H).
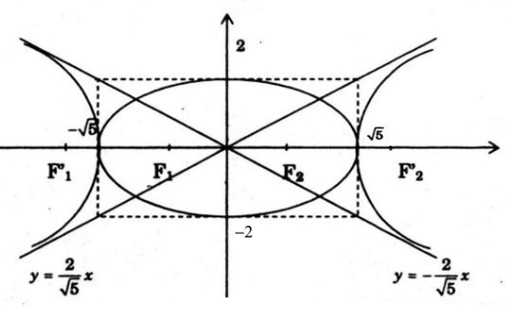
c) Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình
\(\left\{ \matrix{
{{{x^2}} \over 5} + {{{y^2}} \over 4} = 1 \hfill \cr
{{{x^2}} \over 5} - {{{y^2}} \over 4} = 1 \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
{x^2} = 5 \hfill \cr
{y^2} = 0 \hfill \cr} \right.\,\,\,\, \Leftrightarrow \,\,\,\left\{ \matrix{
x = \pm \sqrt 5 \hfill \cr
y = 0 \hfill \cr} \right.\)
Vậy tọa đô giao điểm của (E) và (H) là \(\left( {\sqrt 5 \,;\,0} \right)\) và \(\left( -{\sqrt 5 \,;\,0} \right)\) .
