Advertisements (Quảng cáo)
Cho parabol \((P):{y^2} = 2px.\) Với mỗi điểm M trên (P) (M khác O), gọi M’ là hình chiếu của M trên Oy và I là trung điểm của đoạn OM’. Chứng minh rằng đường thẳng IM cắt parabol đã cho tại một điểm duy nhất.
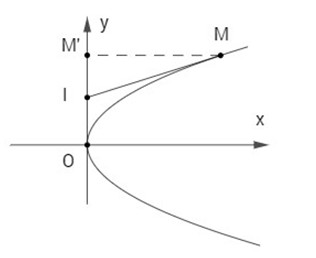
Giả sử \(M({x_o}\,;\,{y_o})\,\, \in \,\,\,(P)\) ta có \(y_o^2 = 2p{x_o}\,({x_o} \ne 0)\) . M’ là hình chiếu của M trên Oy nên \(M'(0\,;\,{y_o})\) , khi đó \(I\left( {0\,;\,{{{y_o}} \over 2}} \right)\,\, \Rightarrow \,\,\overrightarrow {IM} = \left( {{x_o}\,;\,{{{y_o}} \over 2}} \right)\) là vectơ chỉ phương của đường thẳng IM.
Phương trình tham số của IM là
\(\left\{ \matrix{
x = {x_o}.t \hfill \cr
y = {{{y_o}} \over 2} + {{{y_o}} \over 2}.t \hfill \cr} \right.\)
Thay x, y trong phương trình tham số của IM vào phương trình của (P) ta được
\({{y_o^2} \over 4}(1 + {t^2}) = 2p{x_o}t\)
mà \(2p{x_o} = y_o^2\) nên \(y_o^2(1 + {t^2}) = 4y_o^2t\,\,\, \Leftrightarrow \,\,(1 + {t^2}) = 4t\,\,\) ( do \({y_o} \ne 0\))
\(\eqalign{
& \,\, \Leftrightarrow \,\,{(t – 1)^2} = 0\,\,\, \cr
& \,\, \Leftrightarrow \,t = 1 \cr} \)
Vậy IM cắt (P) tại điểm duy nhất \(M({x_o}\,;\,{y_o})\,\) .