Cho đường tròn \((C):\,\,{x^2} + {y^2} = 4\) và điểm A(-2, 3)
a) Viết phương trình của các tiếp tuyến của (C) kể từ A.
b) Tính các khoảng cách từ A đến tiếp điểm của hai tiếp tuyến nói ở câu a) và khoảng cách giữa hai tiếp điểm đó.

Đường tròn (C) có tâm O(0 ; 0), bán kính R=2.
a) Đường thẳng Δ qua A có dạng
\(\eqalign{
& a(x + 2) + b(y - 3) = 0 \cr
& \Leftrightarrow \,ax + by + 2a - 3b = 0 \cr} \)
Δ là tiếp tuyến của (C)
Advertisements (Quảng cáo)
\(\eqalign{
& \Leftrightarrow \,\,d(O\,;\,\Delta ) = R\,\,\, \Leftrightarrow \,\,\,{{|2a - 3b|} \over {\sqrt {{a^2} + {b^2}} }} = 2 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,{(2a - 3b)^2} = 4({a^2} + {b^2}) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,5{b^2} - 12ab = 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\,b(5b - 12a) = 0\cr&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Leftrightarrow \,\,\,\left[ \matrix{
b = 0 \hfill \cr
12a = 5b \hfill \cr} \right. \cr} \)
Với b = 0, chọn a = 1 ta có tiếp tuyến \({\Delta _1}\,\,\,\,x + 2 = 0\)
Với \(12a=5b\), chọn \(a=5, b=12\) ta có tiếp tuyến \({\Delta _2}:\,\,5x + 12y - 26 = 0\)
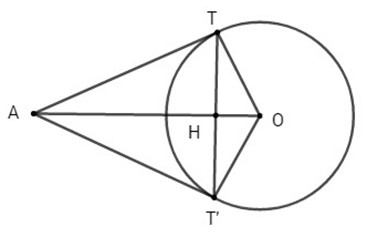
b) Gọi T, T’ là tiếp điểm của \({\Delta _1}\,\,{\Delta _2}\) với (C) . Ta có
\(AT = AT’ = \sqrt {A{O^2} - {R^2}} = \sqrt {13 - 4} = 3\)
Gọi H là giao điểm của TT’ và AO, TH là đường cao của tam giác vuông ATO, ta có
\(\eqalign{
& {1 \over {T{H^2}}} = {1 \over {A{T^2}}} + {1 \over {T{O^2}}} = {1 \over 9} + {1 \over 4} = {{13} \over {36}} \cr
& \Rightarrow \,\,TH = {6 \over {\sqrt {13} }}\,\, \Rightarrow \,\,\,TT’ = 2TH = {{12} \over {\sqrt {13} }} \cr} \)
