Đi một hãng taxi quy định giá thuê xe đi mỗi kilômét là 6 nghìn đồng đối 10 km đầu tiên và 2,5 nghìn đồng đối với các kilômét tiếp theo. Một khách thuê taxi đi quãng đường x kilômét phải trả số tiền là y nghìn đồng. Khi đó, y là một hàm số của đối số x, xác định với mọi x ≥ 0.
a) Hãy biểu diễn y như một hàm số bậc nhất trên từng khoảng ứng với đoạn \([0 ; 10]\) và khoảng \((10 ; +∞)\)
b) Tính f(8), f(10) và f(18).
c) Vẽ đồ thị của hàm số y = f(x) và lập bảng biến thiên cùa nó.

a) Ta có:
Nếu \(x ∈ [0, 10]\) tức hành khách đi không quá 10km thì số tiền phải trả là: \(y = 6x\) (nghìn đồng)
Nếu \(x ∈ (10 ; +∞)\) tức hành khách đi hơn 10km thì số tiền phải trả là:
\(y = 10.6 + (x – 10). 2,5\) (nghìn đồng)
\(\Leftrightarrow y = 2,5x + 35\)
Vậy:
\(y = \left\{ \matrix{
6x\,\,\,\,\,\,;\,\,\,\,0 \le x \le 10 \hfill \cr
2,5x + 35\,\,\,;\,\,\,x > 10 \hfill \cr} \right.\)
b) Ta có:
\(f(8) = 48\)
\(f(10) = 60\)
Advertisements (Quảng cáo)
\(f(18) = 80\)
c) Bảng giá trị:
|
x |
0 |
10 |
|
y = 6x |
0 |
60 |
|
y = 2,5x + 35 |
35 |
60 |
Bảng biến thiên:

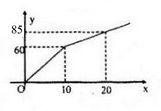
Đồ thị hàm số: