Khi một quả bóng được đá lên sẽ đạt đến độ cao nhất, rồi rơi xuống. Biết rằng quỹ đạo của quả bóng là một parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ độ cao l,2m. Sau đó ls, nó đạt được độ cao 8,5m, và 2s sau khi đá lên, nó ở độ cao 6m (hình dưới đây).
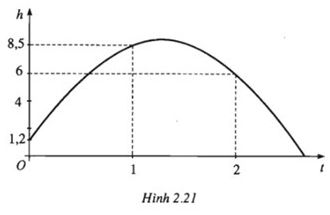
a) Hãy tìm: Hàm số có đồ thị trùng với quỹ đạo của bóng trong tình huống trên.
b) Sau bao lâu thì quả bóng sẽ chạm đất kể từ khi đá lên (chính xác đến hàng phần trăm).
c) Xác định độ cao lớn nhất của quả bóng (tính chính xác đến hàng phần nghìn)
Đáp án:
a) Giả sử \(h = f(t) = at^2 + bt + c (a ≠ 0)\)
Theo đề bài, ta có hệ sau:
\(\left\{ \matrix{
f(0) = 1,2 \hfill \cr
f(1) = 8,5 \hfill \cr
f(2) = 6 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
c = 1,2 \hfill \cr
a + b + c = 8,5 \hfill \cr
4a + 2b + c = 6 \hfill \cr} \right. \)
Advertisements (Quảng cáo)
\(\Leftrightarrow \left\{ \matrix{
c = 1,2 \hfill \cr
a + b = 7,3 \hfill \cr
2a + b = 2,4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = - 4,9 \hfill \cr
b = 12,2 \hfill \cr
c = 1,2 \hfill \cr} \right.\)
Vậy \(h = f(t) = -4,9t^2+ 12,2t + 1,2\)
b) Bóng chạm đất khi:
\(h = 0 \Leftrightarrow - 4,9{t^2} + 12,2t + 1,2 = 0 \)
\(\Leftrightarrow \left\{ \matrix{
t = - 0,09\,\,(l) \hfill \cr
t = 2,58 \hfill \cr} \right.\)
Vậy bóng chạm đất sau gần 2,58 giây
c) Độ cao lớn nhất của quả bóng chính là tung độ đỉnh của parabol chính là:
\({y_0} = - {\Delta \over a} = {{ - 43,09} \over { - 4,9}} \approx 8,794(m)\)
