Bài 1 trang 59 sgk hình học 10: Bài 3. Các hệ thức lượng trong tam giác và giải tam giác. Cho tam giác ABC vuông tại A...
Bài 1. Cho tam giác \(ABC\) vuông tại \(A\), \(\widehat{B}= 58^0\)
và cạnh \(a = 72 cm\). Tính \(\widehat{C}\), cạnh \(b\), cạnh \(c\) và đường cao \(h_a\)

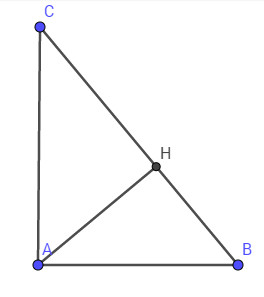
Theo định lí tổng \(3\) góc trong một tam giác ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& \widehat A + \widehat B + \widehat C = {180^0} \cr
& \Rightarrow \widehat C = {180^0} - \widehat A - \widehat B = {180^0} - {90^0} - {58^0} = {32^0} \cr} \)
Xét tam giác vuông \(ABC\) có:
\(b = a.\cos {32^0} \Rightarrow b \approx 61,06cm\);
\(c = a.sin{32^0} \Rightarrow c \approx 38,15cm\)
\(h_a =\frac{b.c}{a}\) \(\Rightarrow h_a ≈ 32,36cm\)
