Bài 6. Cho hình bình hành \(ABCD\) có tâm \(O\). Chứng minh rằng:
a) \(\overrightarrow{CO} - \overrightarrow{OB} = \overrightarrow{BA}\);
b) \(\overrightarrow{AB} - \overrightarrow{BC} = \overrightarrow{DB}\);
c) \(\overrightarrow{DA} -\overrightarrow{DB} = \overrightarrow{OD} - \overrightarrow{OC}\);
d) \(\overrightarrow{DA} - \overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{0}\).

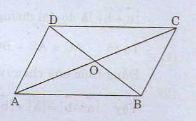
a) Ta có, theo quy tắc ba điểm của phép trừ:
\(\overrightarrow{BA} = \overrightarrow{OA}- \overrightarrow{OB}\) (1)
Mặt khác, \(\overrightarrow{OA} = \overrightarrow{CO}\) (2)
Từ (1) và (2) suy ra:
\(\overrightarrow{BA}= \overrightarrow{CO} - \overrightarrow{OB}\).
Advertisements (Quảng cáo)
b) Ta có : \(\overrightarrow{DB}= \overrightarrow{AB} - \overrightarrow{AD}\) (1)
\(\overrightarrow{AD} = \overrightarrow{BC}\) (2)
Từ (1) và (2) cho ta:
\(\overrightarrow{DB} = \overrightarrow{AB}- \overrightarrow{BC}\).
c) Ta có :
\(\overrightarrow{DA} - \overrightarrow{DB} = \overrightarrow{BA}\) (1)
\(\overrightarrow{OD} - \overrightarrow{OC} = \overrightarrow{CD}\) (2)
\(\overrightarrow{BA} = \overrightarrow{CD}\) (3)
Từ (1), (2), (3) suy ra
\(\overrightarrow{DA} -\overrightarrow{DB} = \overrightarrow{OD} - \overrightarrow{OC}\) đpcm.
d) \(\overrightarrow{DA} - \overrightarrow{DB} + \overrightarrow{DC} = (\overrightarrow{DA} - \overrightarrow{DB}) + \overrightarrow{DC}\)
\(= \overrightarrow{BA}+\overrightarrow{DC} = \overrightarrow{BA}+ \overrightarrow{AB}= \overrightarrow{0}\) ( vì \(\overrightarrow{DC}= \overrightarrow{AB}) \).
