Bài 3. Cho tam giác đều \(ABC\) cạnh \(a\)
a) Cho \(M\) là một điểm trên đường tròn ngoại tiếp tam giác \(ABC\). Tính \(MA^2+ MB^2+ MC^2\) theo \(a\)
b) Cho đường thẳng \(a\) tùy ý, tìm điểm \(N\) trên đường thẳng \(d\) sao cho \(NA^2+ NB^2 + NC^2\) nhỏ nhất
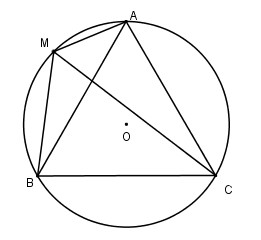
a) Ta có:
\(\eqalign{
& \overrightarrow {MA} = \overrightarrow {OA} - \overrightarrow {OM} \cr
& {\overrightarrow {MA} ^2} = {(\overrightarrow {OA} - \overrightarrow {OM} )^2} = {\overrightarrow {OA} ^2} + {\overrightarrow {OM} ^2} - 2\overrightarrow {OA} .\overrightarrow {OM} \cr
& \Rightarrow {\overrightarrow {MA} ^2} = 2{R^2} - 2\overrightarrow {OA} .\overrightarrow {OM} (1) \cr} \)
Tương tự ta có:
\(\eqalign{
& M{B^2} = {\overrightarrow {MB} ^2} = 2{R^2} - 2\overrightarrow {OB} .\overrightarrow {OM} (2) \cr
& M{C^2} = {\overrightarrow {MC} ^2} = 2{R^2} - 2\overrightarrow {OC.} \overrightarrow {OM} (3) \cr} \)
Từ (1), (2) và (3) suy ra:
\(M{A^2} + M{B^2} + M{C^2} = 6{R^2} - 2\overrightarrow {OM} (\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\)
Tam giác \(ABC\) là tam giác đều nội tiếp đường tròn tâm \(O\) nên \(O\) cũng là trọng tâm của tam giác \(ABC\), cho ta \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow 0\)
Vậy \(M{A^2} + M{B^2} + M{C^2} = 6{R^2} \)
Advertisements (Quảng cáo)
Vì đường tròn ngoại tiếp tam giác đều cạnh \(a\) nên ta có:
\(a = R\sqrt3 ⇒ 6R^2= 2(R\sqrt3)^2\)
Vậy \(M{A^2} + M{B^2} + M{C^2} = 2a^2\)
b) Gọi \(G\) là trọng tâm của tam giác ta có:
\(\eqalign{
& \overrightarrow {NA} = \overrightarrow {NG} + \overrightarrow {GA} \cr
& \Rightarrow {\overrightarrow {NA} ^2} = {\overrightarrow {GA} ^2} + 2\overrightarrow {NG} .\overrightarrow {GA} + {\overrightarrow {GA} ^2} \cr} \)
Tương tự ta có:
\(\eqalign{
& {\overrightarrow {NB} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GB} + {\overrightarrow {GB} ^2} \cr
& {\overrightarrow {NC} ^2} = {\overrightarrow {NG} ^2} + 2\overrightarrow {NG} .\overrightarrow {GC} + {\overrightarrow {GC} ^2} \cr
& \Rightarrow N{A^2} + N{B^2} + N{C^2} = 3N{G^2} + 2\overrightarrow {NG} (\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} ) + G{A^2} + G{B^2} + G{C^2} \cr} \)
Vì \(G\) là trọng tâm của tam giác
⇒ \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\(\eqalign{
& {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} = 3G{A^2} = 3.{({2 \over 3}.{{a\sqrt 3 } \over 2})^2} = {a^2} \cr
& \Rightarrow N{A^2} + N{B^2} + N{C^2} = {a^2} + 3N{G^2} \cr} \)
\(a^2\) là số không đổi nên tổng \(N{A^2} + N{B^2} + N{C^2}\) nhỏ nhất khi \(NG\) đạt giá trị nhỏ nhất. Vì \(NG\) là khoảng cách từ \(G\) đến điểm \(N\) thuộc đường thẳng \(d\) nên \(NG\) nhỏ nhất khi \(NG⊥d\) hay \(N\) là hình chiếu của trọng tâm \(G\) trên đường thẳng \(d\).
