Câu 7 trang 93 SGK Hình học 10: Ôn tập Chương III - Phương pháp tọa độ trong mặt phẳng. Cho đường tròn (C) có tâm I(1, 2) và bán kính bằng 3. Chứng minh rằng tập hợp các điểm M từ đó ta sẽ được hai tiếp tuyến với (C) tạo với nhau một góc 600 là một đường tròn. Hãy viết phương trình đường tròn đó.
Bài 7. Cho đường tròn \((C)\) có tâm \(I(1, 2)\) và bán kính bằng \(3\). Chứng minh rằng tập hợp các điểm \(M\) từ đó ta sẽ được hai tiếp tuyến với \((C)\) tạo với nhau một góc \(60^0\) là một đường tròn. Hãy viết phương trình đường tròn đó.
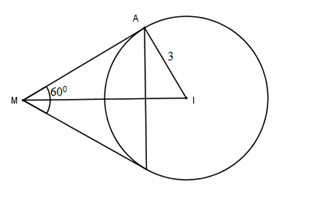
Theo tính chất của tiếp tuyến ta có: \(\widehat {AMI} = {30^0}\)
\(IM = {{IA} \over {\sin \widehat {AMI}}} = {3 \over {\sin {{30}^0}}} = {3 \over {{1 \over 2}}} = 6\)
Advertisements (Quảng cáo)
Gọi tọa độ của \(M\) là \((x ;y)\) Ta có:
\(O{M^2} = {(x - 1)^2} + {(y - 2)^2} = 36\)
Vậy quỹ tích \(M\) là đường tròn tâm \(I (1; 2)\), bán kính \(R = 6\)
Phương trình đường tròn là: \({(x - 1)^2} + {(y - 2)^2} = 36\)