
Cho lục giác đều \(ABCDEF\) nội tiếp trong đường tròn lượng giác (thứ tự đi từ \(A\) đến các đỉnh theo chiều dương). Khi đó, số đo của góc lượng giác \(\left( {OA,OC} \right)\) bằng:
A. \(\frac{{2\pi }}{3} + k2\pi \)
B. \( - \frac{{2\pi }}{3} + k2\pi \)
C. \(\frac{\pi }{3} + k2\pi \)
D. \( - \frac{\pi }{3} + k2\pi \)

Advertisements (Quảng cáo)
Do lục giác đều \(ABCDEF\) nội tiếp trong đường tròn lượng giác tâm \(O\), nên ta có 6 góc bằng nhau: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}\)
Sử dụng hệ thức Chasles để tính số đo của góc lượng giác \(\left( {OA,OC} \right)\)

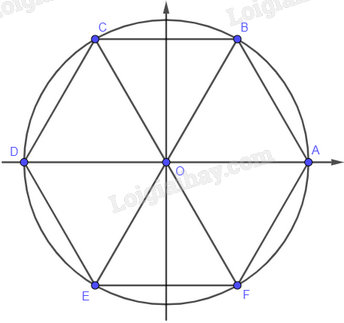
Vì lục giác đều \(ABCDEF\) nội tiếp đường tròn lượng giác tâm \(O\), nên ta có 6 góc bằng nhau: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}\)
Do đó \(\widehat {AOC} = \frac{{2\pi }}{3} \Rightarrow \left( {OA,OC} \right) = \frac{{2\pi }}{3} + k2\pi \)
Đáp án đúng là A.
