Bài 6.22 trang 14 SBT Toán 11 - Kết nối tri thức: Vẽ đồ thị của các hàm số lôgarit sau: \({\rm{lo}}{{\rm{g}}_{\sqrt 3 }}x\) \(y = {\rm{lo}}{{\rm{g}}_{\frac{2}{3}}}x\)...

Vẽ đồ thị của các hàm số lôgarit sau:

a) \({\rm{lo}}{{\rm{g}}_{\sqrt 3 }}x\)

b) \(y = {\rm{lo}}{{\rm{g}}_{\frac{2}{3}}}x\)

Hàm số lôgarit \(y = {\rm{lo}}{{\rm{g}}_a}x\):

• Có tập xác định là \(\left( {0; + \infty } \right)\) và tập giá trị là \(\mathbb{R}\);
• Liên tục trên \(\left( {0; + \infty } \right)\);
• Có đồ thị đi qua các điểm \(\left( {1;0} \right),\left( {a;1} \right)\) và luôn nằm bên phải trục tung.
• Dạng đồ thị của hàm số \(y = {\rm{lo}}{{\rm{g}}_a}x\)
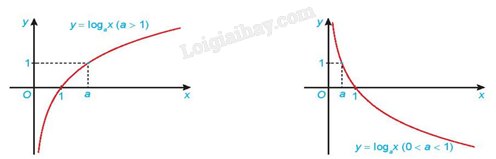
• Vẽ đồ thị hàm số \(y = {\log _a}x\).

  Lập bảng giá trị của hàm số tại một số điểm như sau:

• Xác định các điểm có tọa độ theo bảng trên

  Từ đó, ta vẽ được đồ thị của hàm số \(y = {\log _a}x\)

a) Lập bảng giá trị của hàm số tại một số điểm như sau:

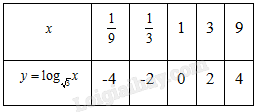
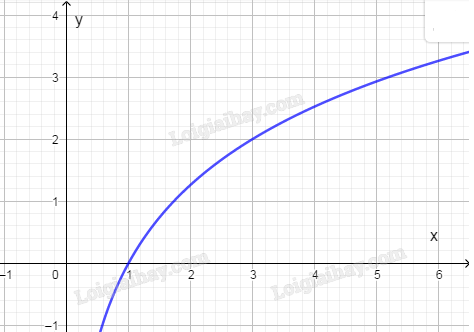
Từ đó, ta vẽ được đồ thị của hàm số \(y = {\rm{lo}}{{\rm{g}}_{\sqrt 3 }}x\) như hình sau;

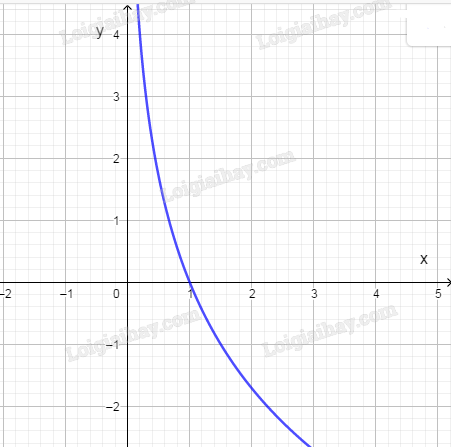
b) Lập bảng giá tri của hàm số tại một số điểm như sau:

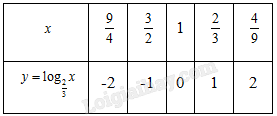
Từ đó, ta vẽ được đồ thị của hàm số \(y = {\rm{lo}}{{\rm{g}}_{\frac{2}{3}}}x\) như hình sau: