
Cho tứ diện \(ABCD\) có \(AC = BC,AD = BD\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng \(\left( {CDM} \right) \bot \left( {ABC} \right)\) và \(\left( {CDM} \right) \bot \left( {ABD} \right)\).

Để chứng minh hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau ta có thể dùng một trong các cách sau:
Chứng minh trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia. \(\left\{ \begin{array}{l}a \subset \left( \alpha \right)\\a \bot \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
Advertisements (Quảng cáo)
+ Áp dụng tính chất trung tuyến của tam giác cân

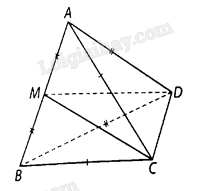
Vì \(M\) là trung điểm của \(AB\) nên \(AB \bot CM\), \(AB \bot DM\), suy ra \(AB \bot \left( {CDM} \right)\).
Vì hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) đều chứa đường thẳng \(AB\) nên \(\left( {ABC} \right) \bot \left( {CDM} \right),\left( {ABD} \right) \bot \left( {CDM} \right)\).
