
Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\). Tính theo \(a\) khoảng cách
a) Giữa hai đường thẳng \(AB\) và \(C’D’\).
b) Giữa đường thẳng \(AC\) và \(\left( {A’B’C’D’} \right)\).
c) Từ điểm \(A\) đường thẳng \(B’D’\).
d) Giữa hai đường thẳng \(AC\) và \(B’D’\).

a)
Bước 1: Xác định đường vuông góc chung hai đường thẳng
Bước 2: Tính độ dài đoạn vuông góc chung hai đường thẳng
Advertisements (Quảng cáo)
b) Vì \(AC\parallel \left( {A’B’C’D’} \right)\) nên \(d\left( {AC,\left( {A’B’C’D’} \right)} \right) = d\left( {A,\left( {A’B’C’D’} \right)} \right) = AA’\).
c) Gọi \(O’\) là giao điểm của \(A’C’\) và \(B’D’\) ta có \(AO’ \bot B’D’\), theo định lý Pythagore áp dụng cho tam giác \(AA’O’\) vuông tại \(A’\) thì \(AO’ = \frac{{a\sqrt 6 }}{2}\).
Do đó, \(d\left( {A,B’D’} \right) = AO’\).
d) Ta có \(d\left( {AC,B’D’} \right) = d\left( {AC,\left( {A’B’C’D’} \right)} \right) = d\left( {A,\left( {A’B’C’D’} \right)} \right) = AA’\).

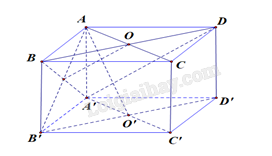
a) Vì \(BC’\) vuông góc với cả hai đường thẳng \(AB\)và \(C’D’\) nên \(d\left( {AB,C’D’} \right) = BC’ = a\sqrt 2 \).
b) Vì \(AC\parallel \left( {A’B’C’D’} \right)\) nên \(d\left( {AC,\left( {A’B’C’D’} \right)} \right) = d\left( {A,\left( {A’B’C’D’} \right)} \right) = AA’ = a\).
c) Gọi \(O’\) là giao điểm của \(A’C’\) và \(B’D’\) ta có \(AO’ \bot B’D’\), theo định lý Pythagore áp dụng cho tam giác \(AA’O’\) vuông tại \(A’\) thì \(AO’ = \frac{{a\sqrt 6 }}{2}\). Do đó, \(d\left( {A,B’D’} \right) = AO’ = \frac{{a\sqrt 6 }}{2}\).
d) Ta có \(d\left( {AC,B’D’} \right) = d\left( {AC,\left( {A’B’C’D’} \right)} \right) = d\left( {A,\left( {A’B’C’D’} \right)} \right) = AA’ = a\).
