
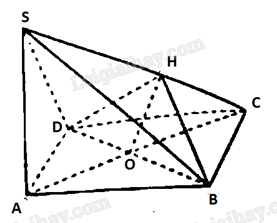
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi tâm \(O\), cạnh bằng \(a\), góc \(BAD\) bằng \({60^ \circ }\). Kẻ \(OH\) vuông góc với \(SC\) tại \(H\). Biết \(SA \bot \left( {ABCD} \right)\) và \(SA = \frac{{a\sqrt 6 }}{2}\). Chứng minh rằng:
a) \(\left( {SBD} \right) \bot \left( {SAC} \right)\);
b) \(\left( {SBC} \right) \bot \left( {BDH} \right)\);
c) \(\left( {SBC} \right) \bot \left( {SCD} \right)\).

Để chứng minh hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau ta có thể dùng một trong các cách sau:
Cách 1. Xác định góc giữa hai mặt phẳng , rồi tính trực tiếp góc đó bằng \({90^0}\).
\(\left( {\widehat {\left( \alpha \right),\left( \beta \right)}} \right) = {90^0} \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
Cách 2.Chứng minh trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia.
\(\left\{ \begin{array}{l}a \subset \left( \alpha \right)\\a \bot \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).
Advertisements (Quảng cáo)
+ Áp dụng tính chất đường chéo của hình thoi vuông góc với nhau

a) Ta có \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot BD\) mà \(BD \bot AC\), do đó \(BD \bot \left( {SAC} \right)\).
Vì mặt phẳng \(\left( {SBD} \right)\) chứa \(BD\) nên \(\left( {SBD} \right) \bot \left( {SAC} \right)\).
b) Ta có \(BD \bot \left( {SAC} \right)\) nên \(BD \bot SC\) mà \(SC \bot OH\), do đó \(SC \bot \left( {BDH} \right)\).
Vì mặt phẳng \(\left( {SBC} \right)\) chứa \(SC\) nên \(\left( {SBC} \right) \bot \left( {BDH} \right)\).
c) Ta có: \(SC = \sqrt {S{A^2} + A{C^2}} = \frac{{3a\sqrt 2 }}{2}\)
Vì \(\Delta CHO\) và \(\Delta CAS\) đồng dạng nên \(\frac{{HO}}{{AS}} = \frac{{CO}}{{CS}}\), suy ra \(HO = \frac{{CO \cdot AS}}{{CS}} = \frac{a}{2} = \frac{{BD}}{2}\).
Do đó, tam giác \(BDH\) vuông tại \(H\), suy ra \(\widehat {BHD} = {90^ \circ }\).
Ta lại có \(BH \bot SC,DH \bot SC\) nên \(\left( {SBC} \right) \bot \left( {SCD} \right)\).
