
Cho tứ diện \(OABC\) có \(OA = OB = OC = a\) và \(\widehat {AOB} = 90^\circ ;\) \(\widehat {BOC} = 60^\circ \); \(\widehat {COA} = 120^\circ \). Tính theo \(a\) thể tích khối tứ diện \(OABC\).

Áp dụng công thức tính thể tích khối chóp: \(S = \frac{1}{3}Bh\).
Trong đó: \(B\) là diện tích đa giác đáy
\(h\) là đường cao của hình chóp
Bước 1: Xác định đường cao của hình chóp \(O.ABC\) có cạnh bên bằng nhau. Chân đường cao là tâm của đáy. Tính chiều cao
Bước 2: Tính diện tích đáy
Advertisements (Quảng cáo)
Bước 3: Tính thể tích khối tứ diện \(V = \frac{1}{3}OH.{S_{ABC}}\)

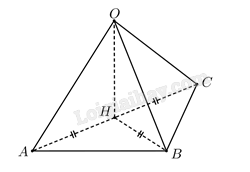
Ta có: \(AB = a\sqrt 2 \), \(BC = a\), \(CA = a\sqrt 3 \), tam giác \(ABC\) vuông tại \(B\).
Kẻ \(OH\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) tại \(H\).
Vì \(OA = OB = OC\) nên \(HA = HB = HC\), hay \(H\) là trung điểm của \(AC\).
Xét tam giác \(OAH\) vuông tại \(H\), theo định lý Pythagore ta tính được: \(OH = \frac{a}{2}\).
Vậy \({V_{OABC}} = \frac{1}{3} \cdot {S_{ABC}} \cdot OH = \frac{1}{3} \cdot \frac{1}{2} \cdot a\sqrt 2 \cdot a \cdot \frac{a}{2} = \frac{{{a^3}\sqrt 2 }}{{12}}{\rm{.\;}}\)
