
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a. Gọi \(M\), N lần lượt là trung điểm các cạnh \(SA,AB\)
a) Tính góc giữa các cặp đường thẳng sau: \(MN\) và \(SD;MO\) và \(SB\)
b) Tính tang của góc giữa hai đường thẳng \(SN\) và \(BC\).

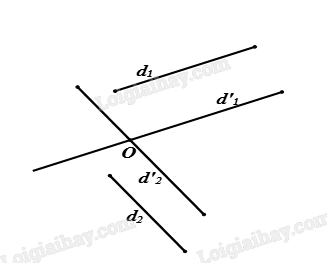
Từ \(O\) dựng các đường thẳng \(d’_1,d’_2\) lần lượt song song có thể trùng nếu \(O\) nằm trên một trong hai đường thẳngvới \({d_1}\) và \({d_2}\). Góc giữa hai đường thẳng \(d’_1,d’_2\)chính là góc giữa hai đường thẳng\({d_1},{d_2}\).
Lưu ý :
Áp dụng định lý Pytago đảo để chứng minh tam giác vuông
Áp dụng tính chất đường trung bình tam giác
Advertisements (Quảng cáo)
Áp dụng tính chất \(\left\{ \begin{array}{l}a//b\\a \bot c\end{array} \right. \Rightarrow b \bot c\)

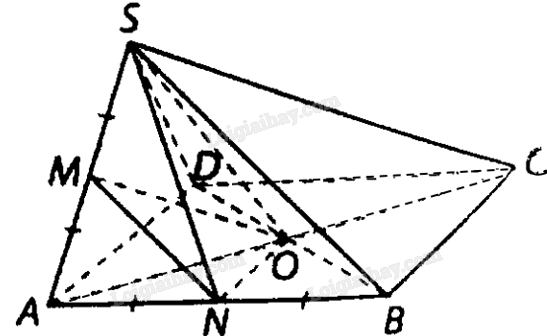
a) Ta có: \(B{D^2} = S{B^2} + S{D^2} = 2{a^2}\) nên \(\Delta SBD\) vuông tại \(S\), mà \(MN//SB\), suy ra \(\left( {MN,SD} \right) = \left( {SB,SD} \right) = {90^ \circ }\).
Với O là giao điểm của \(AC\) và \(BD\) thì \(MO//SC\).
Khi đó \(\left( {MO,SB} \right) = \left( {SC,SB} \right) = \widehat {BSC} = {60^ \circ }\).
b) Vì \(ON{\rm{ }}//BC\) nên \(\left( {SN,BC} \right) = \left( {SN,ON} \right) = \widehat {SNO}\).
Ta có \(SO = \frac{{a\sqrt 2 }}{2};ON = \frac{a}{2}\) và tam giác \(SNO\)vuông tại O nên \({\rm{tan}}\widehat {SNO} = \frac{{SO}}{{ON}} = \sqrt 2 \).
Vậy \({\rm{tan}}\left( {SN,BC} \right) = \sqrt 2 \).
