Cho đường thẳng a và vectơ \(\overrightarrow u \) có giá vuông góc với a. Gọi F là phép hợp thành của đối xứng trục Đa. Gọi F là phép hợp thành của đối xứng trục Đa và tịnh tiến \({T_{\overrightarrow u }}\). Với điểm M bất kì, gọi M’ = F(M) và I là trung điểm của MM’.
a) Tìm quỹ tích của I khi M thay đổi.
b) Chứng minh rằng F là phép đối xứng trục.

Advertisements (Quảng cáo)
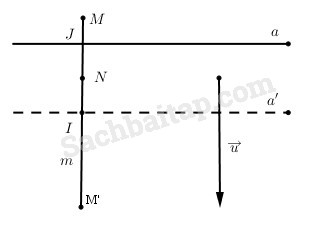
a) Nếu Đa biến điểm M thành N thì \({T_{\overrightarrow u }}\) biến điểm N thành điểm M’ tức là \(\overrightarrow {NM’} = \overrightarrow u \). Vì vectơ \(\overrightarrow u \) có giá vuông góc với a nên ba điểm M, N và M’ cùng nằm trên đường thẳng m vuông góc với a. Gọi J là trung điểm của MN thì J nằm trên a và ta có :
\(\eqalign{ & \overrightarrow {JI} = \overrightarrow {MI} - \overrightarrow {MJ} = {1 \over 2}\left( {\overrightarrow {MM’} - \overrightarrow {MN} } \right) \cr & = {1 \over 2}\overrightarrow {NM’} = {{\overrightarrow u } \over 2}. \cr} \)
Như vậy I là ảnh của J qua phép tịnh tiến theo vectơ \({{\overrightarrow u } \over 2}\), suy ra quỹ tích I là đường thẳng a’ ảnh của a qua phép tịnh tiến đó.
b) Từ câu a), ta suy ra a’ là trung trực của đoạn thẳng MM’. Suy ra F là phép đối xứng trục với trục là đường thẳng a’.
