31. Trang 10 Sách bài tập Hình Học 11 nâng cao.
Chứng minh rằng hợp thành của một số phép quay với các tâm quay trùng nhau là một phép quay.

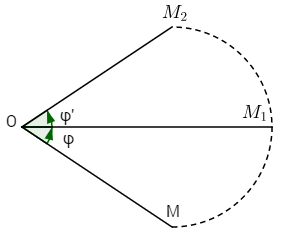
Giả sử Q và Q’ là hai phép quay có tâm O với góc quay lần lượt là \(\varphi \) và \(\varphi ‘,\) còn F là hợp thành của Q và Q’. Với mọi điểm M khác O, giả sử Q biến M thành \({M_1}\) và Q’ biến \({M_1}\) thành \({M_2}\). Khi đó ta có:
\(\eqalign{
& OM = O{M_1} = O{M_2} \cr
& \left( {OM,O{M_1}} \right) = \varphi ,\,\left( {O{M_1},O{M_2}} \right) = \varphi ‘ \cr} \)
Suy ra \(OM = O{M_2}\)
Advertisements (Quảng cáo)
Và \(\left( {OM,O{M_2}} \right) = \left( {OM,O{M_1}} \right) + \left( {O{M_1},O{M_2}} \right) \)
\(= \varphi + \varphi ‘\)
Vậy hợp thành F là phép quay tâm O góc quay bằng \(\varphi + \varphi ‘\)
Từ đó suy ra: Hợp thành của một số hữu hạn có tâm trùng nhau là một phép quay với tâm đó và có góc quay bằng tổng các góc quay của các phép quay đã cho.