43. Trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là một tứ giác lồi. M là trung điểm của cạnh bên SA, N là trung điểm của cạnh bên SC.
a) Xác định các thiết diện của hình chóp khi cắt bởi các mặt phẳng lần lượt qua M, N và song song với mp(SBD).
b) Gọi I, J là giao điểm của hai mặt phẳng nói trên với AC. Chứng minh rằng \(IJ = {1 \over 2}AC\).

a)
Advertisements (Quảng cáo)
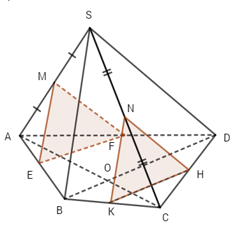
Giả sử (P) là mặt phẳng qua M và song song với mp(SBD) và E, F là giao điểm của (P) với các cạnh AB và AD. Khi đó, dễ thấy ME // SB, MF // SD và EF // BD. Vậy thiết diện của hình chóp khi cắt bởi mặt phẳng qua M và song song với mp(SBD) là tam giác MEF.
Tương tự, thiết diện của hình chóp khi cắt bởi mặt phẳng qua N và song song với mp(SBD) là tam giác NKH với NK // SB, NH // SD, KH // BD.
b) I, J lần lượt là giao điểm của hai mặt phẳng (MEF), (NKH) với AC cũng chính là giao điểm của EF, KH với AC. Do M là trung điểm của SA và ME // SB, MF // SD nên E, F lần lượt là trung điểm của AB và AD. Từ đó suy ra I là trung điểm của AO, (ở đây O là giao điểm của AC và BD).
Vậy \(IO = {1 \over 2}AO\)
Tương tự \({\rm{OJ}} = {1 \over 2}OC\). Vậy \({\rm{IJ}} = {1 \over 2}AC\)
