Advertisements (Quảng cáo)
46. Trang 59 Sách Bài tập Hình học 11 Nâng cao
Cho hình chóp S.ABCD đáy là hình thang (AB // CD). Điểm M thuộc cạnh BC không trùng với B và C.
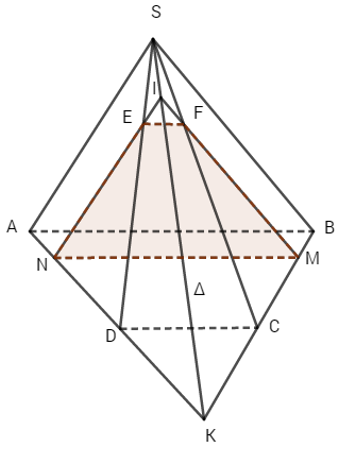
a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P) qua M và song song với mp(SAB). Thiết diện là hình gì?
b) Gọi E và F lần lượt là giao điểm của mp(P) với SD và SC. Chứng minh rằng giao điểm I của NE và MF chạy trên một đường thẳng cố định.
(h.99)
a) \(\left. \matrix{
\left( P \right)//\left( {SAB} \right) \hfill \cr
\left( P \right) \cap \left( {ABCD} \right) = MN \hfill \cr
\left( {SAB} \right) \cap \left( {ABCD} \right) = AB \hfill \cr} \right\} \Rightarrow MN//AB\,\,(1)\)
\(\left. \matrix{
\left( P \right)//\left( {SAB} \right) \hfill \cr
\left( P \right) \cap \left( {SBC} \right) = MF \hfill \cr
\left( {SAB} \right) \cap \left( {SBC} \right) = SB \hfill \cr} \right\} \Rightarrow MF//SB\,\,(2)\)
Advertisements (Quảng cáo)
\(\left. \matrix{
\left( P \right)//\left( {SAB} \right) \hfill \cr
\left( P \right) \cap \left( {SAD} \right) = NE \hfill \cr
\left( {SAB} \right) \cap \left( {SAD} \right) = SA \hfill \cr} \right\} \Rightarrow NE//SA\,\,(3)\)
\(\left. \matrix{
\left( P \right)//CD \hfill \cr
CD \subset \left( {SCD} \right) \hfill \cr
\left( P \right) \cap \left( {SCD} \right){\rm{ = EF}} \hfill \cr} \right\} \Rightarrow EF//CD\,\,(4)\)
Các điểm N, E, F được xác định bởi (1), (2), (3), (4) là giao điểm của (P) với AD, SD, SC có tính chất EF // MN. Vậy thiết diện là hình thang MNEF.
b) Xét ba mặt phẳng (P), (SAD), (SBC). Ta có:
\(\eqalign{
& \left( P \right) \cap \left( {SAD} \right) = NE \cr
& \left( P \right) \subset \left( {SBC} \right) = MF \cr
& \left( {SAD} \right) \cap \left( {SBC} \right){\rm{ = }}\Delta \cr} \)
Vậy ba đường thẳng NE, MF, \(\Delta \) đồng quy tại I (I là giao điểm của NE và MF). Từ đó, điểm I chạy trên đường thẳng \(\Delta \) cố định.