Cho hình chóp tam giác đều S.ABC cạnh đáy bằng a, đường cao SO = 2a. Gọi M là điểm thuộc đường cao AA1 của tam giác ABC. Xét mặt phẳng (P) đi qua M và vuông góc với AA1. Đặt AM = x.
a) Xác định thiết diện của hình chóp khi cắt bởi mp(P).
b) Tính diện tích thiết diện vừa xác định theo a và x. Xác định vị trí điểm M để diện tích thiết diện đó đạt giá trị lớn nhất.

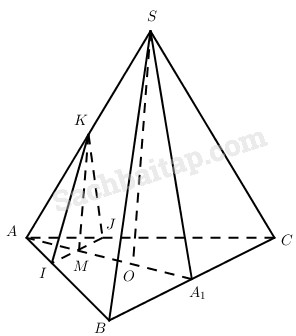
a) Vì \(SO \bot A{A_1},BC \bot A{A_1},\left( P \right) \bot A{A_1}\) và (P) qua điểm M nên (P) là mặt phẳng đi qua điểm M và song song với SO, BC.
Trường hợp x = 0, thiết diện là điểm A.
Trường hợp \(0 < x \le {{a\sqrt 3 } \over 3}\)
\(\left( P \right) \cap \left( {ABC} \right) = IJ\), IJ đi qua điểm M và IJ // BC.
\(\left( P \right) \cap \left( {SAO} \right) = MK,MK// SO\)
Vậy thiết diện của hình chóp S.ABC khi cắt bởi (P) là tam giác IKJ. Dễ thấy IKJ là tam giác cân tại K.
Trường hợp \({{a\sqrt 3 } \over 3} < x < {{a\sqrt 3 } \over 2}\)
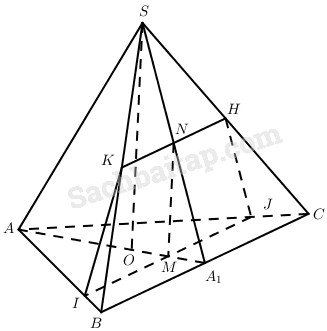
\(\left( P \right) \cap \left( {ABC} \right) = IJ\), IJ đi qua M và IJ // BC.
\(\left( P \right) \cap \left( {SO{A_1}} \right) = MN,MN\parallel SO\)
\(\left( P \right) \cap \left( {SBC} \right) = HK\), HK đi qua N và HK // BC.
Vậy thiết diện thu được là hình thang IJHK.
Mặt khác M, N lần lượt là trung điểm của IJ, HK; MN // SO; \(SO \bot \left( {ABC} \right)\) nên \(MN \bot IJ\). Vậy tứ giác IJHK là hình thang cân.
Advertisements (Quảng cáo)
Trường hợp \(x = {{a\sqrt 3 } \over 2}\), thiết diện là đoạn thẳng BC.
b) Trường hợp \(0 \le x \le {{a\sqrt 3 } \over 3}\)
\(\eqalign{ & {S_{IJK}} = {1 \over 2}IJ.MK \cr & {{IJ} \over {BC}} = {{AM} \over {A{A_1}}} \Rightarrow IJ = {{2x\sqrt 3 } \over 3} \cr & {{MK} \over {SO}} = {{AM} \over {AO}} \Rightarrow MK = 2x\sqrt 3 \cr} \)
Vậy \({S_{{\rm{IJ}}K}} = 2{{\rm{x}}^2}\)
Trường hợp \({{a\sqrt 3 } \over 3} < x < {{a\sqrt 3 } \over 2}\)
\({S_{{\rm{IJ}}HK}} = {1 \over 2}\left( {{\rm{IJ}} + HK} \right).MN\)
Ta có:
\(\eqalign{ & IJ = {{2x\sqrt 3 } \over 3} \cr & {{HK} \over {BC}} = {{SN} \over {S{A_1}}} = {{OM} \over {O{A_1}}} \Rightarrow HK = 2\left( {x\sqrt 3 - a} \right); \cr & {{MN} \over {SO}} = {{M{A_1}} \over {{A_1}O}} \Rightarrow MN = 2\left( {3{\rm{a}} - 2x\sqrt 3 } \right) \cr} \)
Vậy \({S_{{\rm{IJ}}HK}} = {2 \over 3}\left( {4{\rm{x}}\sqrt 3 - 3{\rm{a}}} \right)\left( {3{\rm{a}} - 2x\sqrt 3 } \right)\)
Dễ thấy khi \(0 < x \le {{a\sqrt 3 } \over 3}\) thì diện tích thiết diện lớn nhất khi và chỉ khi \(x = {{a\sqrt 3 } \over 3}\). Lúc đó diện tích thiết diện bằng \({{2{{\rm{a}}^2}} \over 3}\).
Khi \({{a\sqrt 3 } \over 3} < x < {{a\sqrt 3 } \over 2}\) thì diện tích thiết diện là:
\({S_{{\rm{IJHK}}}} = {1 \over 3}\left( {4{\rm{x}}\sqrt 3 - 3{\rm{a}}} \right)\left( {6{\rm{a}} - 4{\rm{x}}\sqrt 3 } \right)\).
Từ đó, suy ra diện tích thiết diện lớn nhất khi và chỉ khi \(x = {{3{\rm{a}}\sqrt 3 } \over 8}\) .
Lúc đó diện tích thiết diện bằng \({{3{{\rm{a}}^2}} \over 4}\).
Vậy khi M thay đổi trên AA1 thì diện tích thiết diện lớn nhất bằng \({{3{{\rm{a}}^2}} \over 4}\), lúc đó M được xác định bởi:
\(AM = x = {{3{\rm{a}}\sqrt 3 } \over 8}\) hay \({{AM} \over {A{A_1}}} = {3 \over 4}\).
