Cho hai mặt phằng (P) và (Q) vuông góc với nhau theo giao tuyến ∆. Lấy hai điểm A, B cố định thuộc ∆ sao cho AB = a. Gọi SAB là tam giác đều trong (P), ABCD là hình vuông nằm trong (Q).
a) Tính góc giữa mặt phẳng (SCD) với các mặt phẳng (P) và (Q).
b) Gọi O1 là giao điểm của hai đường thẳng B1C và A1D, ở đó A1, B1 tương ứng là các trung điểm của SA, SB. Gọi H1 là giao điểm của đường cao SH của tam giác SAB với mp(A1B1CD). Chứng minh rằng SO1 vuông góc với SA và CD. Tính góc giữa mp(A1B1O1) với các mặt phẳng (P) và (Q).

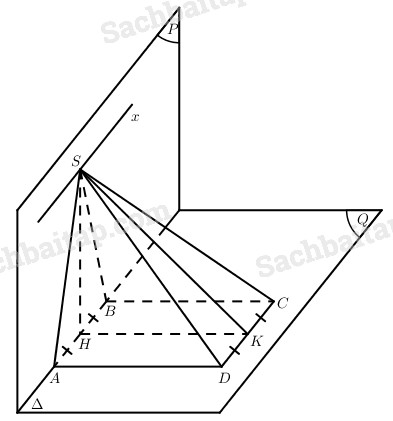
a) Dễ thấy mp(SCD) cắt (P) theo giao tuyến Sx, Sx // AB.
Gọi H và K lần lượt là trung điểm của AB và CD thì \(S{\rm{x}} \bot mp\left( {SHK} \right)\) và tam giác SHK vuông tại H, Suy ra \(\widehat {H{\rm{S}}K}\) là góc giữa hai mặt phẳng (SDC) và (P). Ta có:
\(\tan \widehat {H{\rm{S}}K} = {{HK} \over {H{\rm{S}}}} = {a \over {{{a\sqrt 3 } \over 2}}} = {{2\sqrt 3 } \over 3}\)
Vậy nếu gọi φ là góc giữa hai mặt phẳng (SDC) và (P) thì φ là góc thỏa mãn:
\(\tan \varphi = {{2\sqrt 3 } \over 3}\)
Tương tự như trên thì \(\widehat {HK{\rm{S}}}\) là góc giữa hai mặt phẳng (SCD) và (Q).
Ta có: \(\tan \widehat {HK{\rm{S}}} = {{a\sqrt 3 } \over {2{\rm{a}}}} = {{\sqrt 3 } \over 2}\) .
Advertisements (Quảng cáo)
b)
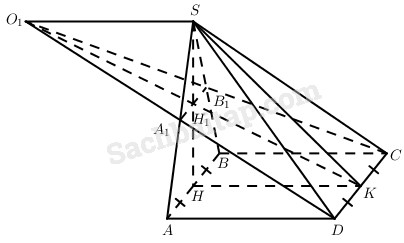
Dễ thấy ba điểm O1, H1, K thẳng hàng (do H1 là giao điểm của SH với A1B1) và \({H_1}{O_1} = {H_1}K\). Mặt khác \({H_1}S = {H_1}H\). Suy ra O1S // HK.
Do \(HK \bot AB\) và \(\left( {SAB} \right) \bot \left( {ABC{\rm{D}}} \right)\) nên \(HK \bot \left( {SAB} \right)\).
Vậy \({O_1}S \bot \left( {SAB} \right)\), từ đó \({O_1}S \bot AB\) và \({O_1}S \bot SA\).
Vì AB // CD, từ đó \({O_1}S \bot SA\) và \({O_1}S \bot C{\rm{D}}\)
Góc giữa hai mặt phẳng (A1B1O1) và (Q) chính là \(\widehat {{H_1}KH}\).
\(\tan \widehat {{H_1}KH} = {{H{H_1}} \over {HK}} = {{a\sqrt 3 } \over {4{\rm{a}}}} = {{\sqrt 3 } \over 4}\)
Góc giữa hai mặt phẳng (A1B1O1) và (P) chính là \(\widehat {H{H_1}K}\).
Ta có \(\tan \widehat {H{H_1}K} = {{HK} \over {H{H_1}}} = {a \over {{{a\sqrt 3 } \over 4}}} = {{4\sqrt 3 } \over 3}\).
