Cho hình lăng trụ đều ABC.A’B’C’ cạnh đáy bằng a, chiều cao bằng h. Điểm M thuộc đoạn AB’ sao cho \({{MA} \over {MB’}} = {5 \over 4}\).
a) Tính góc giữa hai đường thẳng AC và BC’.
b) Một mặt phẳng (P) đi qua điểm M và song song với các đường thẳng A’C và BC’ cắt đường thẳng CC’ tại C1, tính tỉ số \({{{C_1}C} \over {{C_1}C’}}\).

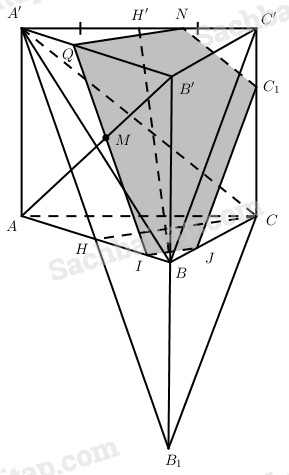
a) Vì AC // A’C’ nên góc giữa AC và BC’ bằng góc giữa A’C’ và BC’.
Gọi H’ là trung điểm của A’C’, do BA’ = BC’ nên \(\widehat {BH’C’} = {90^0}\). Vậy \(\widehat {H’C’B}\) là góc giữa hai đường thẳng AC và BC’. Đặt \(\widehat {H’C’B} = \alpha \) thì \(\cos \alpha = {{H’C’} \over {BC’}} = {a \over {2\sqrt {{h^2} + {a^2}} }}\).
Vậy góc giữa AC và BC’ là α mà \(\cos \alpha = {a \over {2\sqrt {{h^2} + {a^2}} }}\).
b) Lấy B1 thuộc B’B sao cho BB’ = BB1, khi đó CB1 // C’B. Vậy mp(P) đi qua M, song song với BC’ và A’C chính là mặt phẳng đi qua điểm M và song song với mp(A’CB1).
Advertisements (Quảng cáo)
Dễ thấy mp(A’CB1) cắt hình lăng trụ đã cho theo thiết diện là A’HC còn (P) cắt lăng trụ ABC.A’B’C’ theo thiết diện IJC1NQ, trong đó IQ là đường thẳng đi qua điểm M và song song với A’H, còn \(IJ//HC,J{C_1}//BC’,{C_1}N//A’C\) .
Ta cos \({{{C_1}C} \over {{C_1}C’}} = {{CJ} \over {BJ}} = {{HI} \over {IB}}\)
Đặt \(HI = x\). Do \({{MA} \over {MB’}} = {5 \over 4}\) nên \({{AI} \over {B’Q}} = {5 \over 4}\)
hay
\(\eqalign{ & {{{a \over 2} + x} \over {a - x}} = {5 \over 4} \cr & \Rightarrow 2{\rm{a}} + 4{\rm{x}} = 5{\rm{a}} - 5{\rm{x}} \Rightarrow x = {a \over 3} \cr} \)
Khi đó \(IB = {a \over 2} - {a \over 3} = {a \over 6}\)
Vậy \({{{C_1}C} \over {{C_1}C’}} = {{{a \over 3}} \over {{a \over 6}}} = 2\).
