Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Xét tứ diện AB’CD’. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mp(ABC). Tính diện tích thiết diện thu được. Hãy xét kết quả của toán khi ABCD.A’B’C’D’ là hình hộp chữ nhật với ba kích thước là a, b, c.

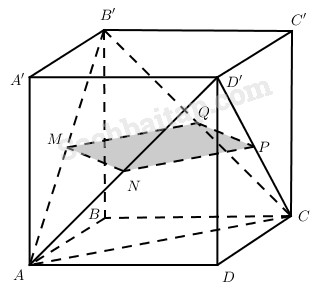
Vì hình ABCD.A’B’C’D’ là hình lập phương nên AB’CD’ là tứ diện đều có cạnh \(a\sqrt 2 \) (a là cạnh của hình lập phương). Dễ thấy thiết diện là tứ giác MNPQ, trong đó M, N, P, Q lần lượt là trung điểm của các cạnh AB’, AD’, D’C, B’C. Do AB’CD’ là tứ diện đều nên \(B’D’ \bot AC\).
Vậy tứ giác MNPQ là hình vuông cạnh bằng \({{a\sqrt 2 } \over 2}\). Từ đó \({S_{MNPQ}} = {{{a^2}} \over 2}\)
Chú ý. Có thể chiếu tứ giác MNPQ xuống mặt phẳng (ABCD) theo phương chiếu A’A được tứ giác \({M_1}{N_1}{P_1}{Q_1}\) trong đó \({M_1},{N_1},{P_1},{Q_1}\) lần lượt là trung điểm của AB, AD, CD, BC và
Advertisements (Quảng cáo)
\({S_{MNPQ}} = {S_{{M_1}{N_1}{P_1}{Q_1}}} = {1 \over 2}{S_{ABC{\rm{D}}}} = {{{a^2}} \over 2}\).
Nếu hình lập phương ABCD.A’B’C’D’ được thay bởi hình hộp chữ nhật với \(AB = a,BC = b,AA’ = c\) thì thiết diện thu được vẫn là tứ giác MNPQ và MNPQ là hình thoi có độ dài hai đường chéo MP và NQ lần lượt là b, a. Do đó:
\({S_{MNPQ}} = {{ab} \over 2}\).
Chú ý. Thực hiện như phần chú ý ở trên thì
\({S_{MNPQ}} = {S_{{M_1}{N_1}{P_1}{Q_1}}} = {1 \over 2}{S_{ABC{\rm{D}}}} = {{ab} \over 2}\).
