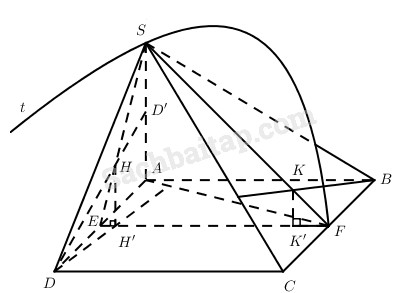
Trong mp(P), cho hình chữ nhật ABCD với AB = b, BC = a. Gọi E, F lần luợt là trung điểm của AD và BC. Trong mặt phẳng qua EF và vuông góc với (P) vẽ nửa đường tròn đường kính (EF). Gọi S là điểm bất kì trên nửa đường tròn đó.
a) Chứng minh rằng mp(SEF) vuông góc với hai mặt phẳng (SAD), (SBC) và mp(SAD) vuông góc với mp(SBC).
b) Gọi H’, K’ lần lượt là hình chiếu của các trực tâm H và K của các tam giác SAD và SBC xuống (P). Chứng minh rằng HH’.KK’ không phụ thuộc vào vị trí điểm S.

a) Vì \(\left( {SEF} \right) \bot \left( {ABCD} \right)\) và \(A{\rm{D}} \bot {\rm{EF}}\)
nên \(AD \bot \left( {SEF} \right)\)
Từ đó \(\left( {SEF} \right) \bot \left( {SAD} \right)\).
Tương tự \(\left( {SEF} \right) \bot \left( {SBC} \right)\)
Dễ thấy \(\left( {SA{\rm{D}}} \right) \cap \left( {SBC} \right) = St,St//A{\rm{D}}.\)
Do \(AD \bot \left( {SEF} \right)\), từ đó \(St \bot \left( {SEF} \right)\), tức là \(\widehat {ESF}\) hoặc \({180^0} - \widehat {ESF}\) là góc giữa hai mặt phẳng (SAD) và (SBC).
Vì S thuộc đường tròn đường kính EF nên \(\widehat {ESF} = {90^0}\)
Vậy \(\left( {SA{\rm{D}}} \right) \bot \left( {SBC} \right)\)
Advertisements (Quảng cáo)
b) Kẻ \(DD’ \bot SA\)
Do
\(\eqalign{ & SF \bot \left( {SAD} \right) \Rightarrow SF \bot DD’ \cr & \Rightarrow DD’ \bot \left( {SAF} \right) \Rightarrow DD’ \bot AF \cr} \)
Mặt khác \(HH’ \bot \left( {ABC{\rm{D}}} \right)\) nên \(DH’ \bot AF\) (định lí ba đường vuông góc).
Ta lại có H’ thuộc EF. Vậy H’ là trực tâm tam giác ADF, từ đó H’ cố định. Tương tự K’ cũng là điểm cố định.
Ta có ∆HH’E đồng dạng ∆FK’K, do đó
\({{HH’} \over {K’F}} = {{H’E} \over {K’K}} \Rightarrow HH’.KK’ = H’E.K’F\)
Như vậy HH’.KK’ không đổi
Thật vậy, ∆EDH’ đồng dạng ∆EFA \( \Rightarrow {{EH’} \over {E{\rm{A}}}} = {{DE} \over {F{\rm{E}}}} \Rightarrow EH’ = {{{a^2}} \over {4b}}\).
Tương tự, ta cũng có \(FK’ = {{{a^2}} \over {4b}}\)
Vậy \(HH’.KK’ = {{{a^4}} \over {16{b^2}}}\) không đổi.
